竞赛图

Posted 2021-03-07 amitherblogs

竞赛图是通过在无向完整图中为每个边缘分配方向而获得的有向图。

转自：https://www.cnblogs.com/acha/p/9042984.html

定理 1

竞赛图强连通缩点后的DAG呈链状, 前面的所有点向后面的所有点连边

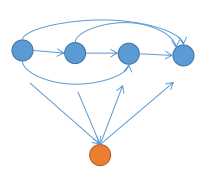
定理 2

竞赛图的强连通块 存在一条哈密顿回路

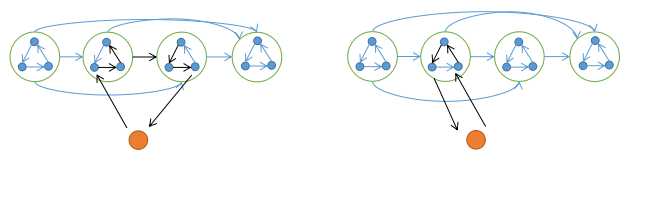
定理 3

竞赛图存在一条 哈密顿路径

证明 : 如图示方法构造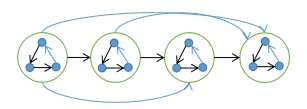

引理

竞赛图里, 大小为 n>1n>1 的强连通块中, 大小为 [3,n][3,n] 的简单环均存在

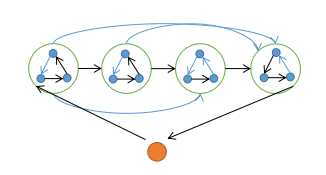
定理4

竞赛图判定定理 Landau‘s Theorem:
令sisi为第ii个点的出度 (竞赛中获胜的积分)
对ss排好序后, 若满足 ∑ki=1si≥(k2)且∑s=(n2)∑i=1ksi≥(k2)且∑s=(n2) , 定能构造出一种竞赛图, 反之不能

 

UCF Local Contest 2015

I Longest path

题意：给出一个??(?? ≤ 500)个点的有向图，任意两个点之间有且仅一条有向边。 求一条不重复经过一个点的最长的简单路径。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=1e9+7;
const int inf=0x3f3f3f3f;
const int maxn=1e5+7;
list<int> List;
int Matrix[505][505];
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int N;
        List.clear();
        for(int i=1;i<=N;++i)
            for(int j=1;j<=N;++j)
                scanf("%d",&Matrix[i][j]);
        List.push_back(1);
        for(int i=2;i<=N;++i){
            int CountIn=0,CountOut=0;
            for(auto it:List){
                if(Matrix[i][it]) ++CountOut;
                else ++CountIn;
            }
            if(CountOut==i-1) List.push_front(i);//加入列头 
            else if(CountIn==i-1) List.push_back(i);//加入列尾 
            else{//找到(u,v)(v,w) 
                auto it=List.begin();
                for(;it!=List.end();++it){
                    auto Next=it;++Next;
                    if(Next==List.end()) break;
                    if(Matrix[*it][i] && Matrix[i][*Next]) break;
                }
                List.insert(++it,i);
            }
        }
        int Count=0;
        for(auto it:List){
            ++Count;
            printf("%d",it);
            if(Count<N) printf(" ");
        }
        printf("
");
    }
    return 0;
}