已知前序中序求后续；已知中序后序求前序；

Posted 2021-03-07 wangqiqq

后序遍历与中序遍历，求前序遍历

首先，一点基本常识，给你一个后序遍历，那么最后一个就是根（同理前序遍历，第一个是根）

那么这个算法的核心就是不断的求根；

接下来我用一个实例来说明怎样进行求根：

 

 

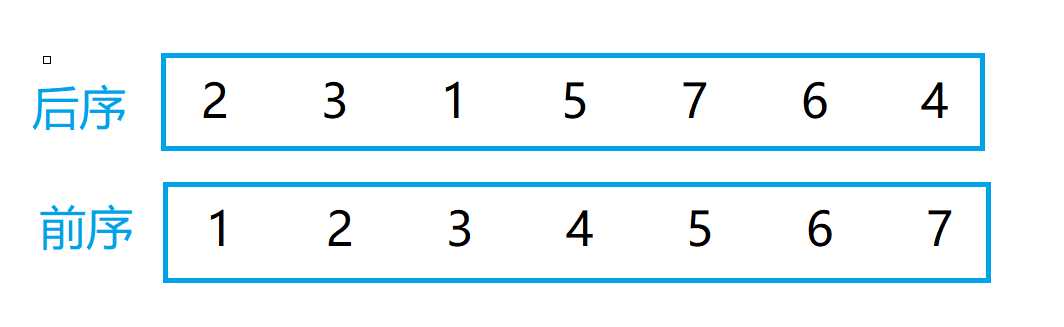
 例如以上，给出后序遍历和中序遍历，求前序遍历

首先根据后序遍历的最后一个就是根，可以知道4是根，以此可将前序和后序都分为三部分；

 

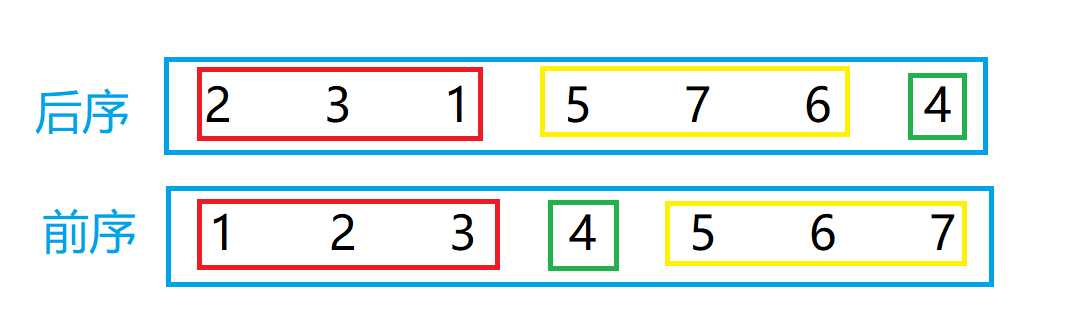
看上图，在前序遍历中，绿色框中的4为根，则在4的左边，红色框的就为以4为根的左子树，黄色框的就是以4为根的右子树。

则在找到4这个根之后，此题可以转换为两个子问题，一下：

求红框的前序列，求黄框的前序列。

之后就可以递归了；我们再回到上面的图，再进行一个小小的思考；

观察前序遍历和后序遍历，都可以由三部分组成，红框的左子树，黄框的右子树以及绿框的根；

那么，在进行函数递归的时候，重点就是怎样计算各个部分的下标起始，来让程序可以递归下去；

上代码：

方法一：

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
void beford(string in,string after){
    if (in.size()>0){
        char ch=after[after.size()-1];
        cout<<ch;//找根输出
        int k=in.find(ch);
        beford(in.substr(0,k),after.substr(0,k));
        beford(in.substr(k+1),after.substr(k,in.size()-k-1));//递归左右子树；
    }
}
int main(){
    string inord,aftord;
    cin>>inord;cin>>aftord;//读入
    beford(inord,aftord);cout<<endl;
    return 0;
}

上面代码的关键是，用substr函数将字符串进行切割，以此来达到分离字符串三部分的操作比较好理解。

方法二：

#include<iostream>
using namespace std;
int a[35],b[35];
void build(int l1,int r1,int l2,int r2)
{
    if(l1>r1) return;
    cout<<" "<<b[r2];
    int p = l1;
    while(a[p]!=b[r2])
    {
        p++;
    }
    int cnt = p - l1;
    build(l1,p-1,l2,l2+cnt-1);
    build(p+1,r1,l2+cnt,r2-1);
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>b[i];
    }
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
    }
    build(0,n-1,0,n-1);
} 

和上面的方法核心思想是不变的，但是有一点差别是，传入函数的不再是序列整体，而是用左右下标的方式来进行递归；

特别注意，函数中的 cnt = p-l1, cnt是左子树的长度，及黄框的长度，以此来进行递归；

已知前序和中序求后序的操作和以上一样，只是将递归和查询的位置变化就ok；

以上。可能讲的有点恍惚，有不懂的请评论留言；