322.零钱兑换（动态规划）

Posted 2021-03-07 cheviszhang

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

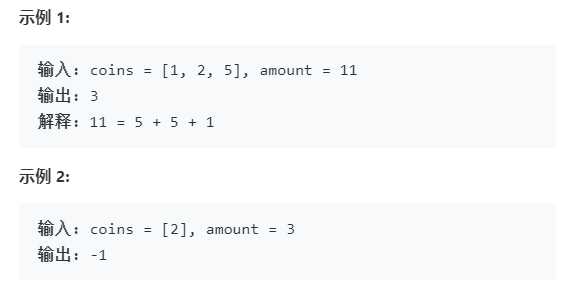
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/coin-change
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 

以前我会直接贪婪算法，然后解不出来，现在第一想法就是动态规划：把每一步的最优解都算出来，取最后一项返回。

本题状态转移方程： dp[ i ] =  min(dp[ i - coins[ j ]],......) 

　　特判：1.i - coins[ j ]<0: continue

　　　　    2.if dp[ i - coins[ j ]] == -1: continue  并且 j 对应的dp[ i - coins[ j ]]不加入状态转移方程中的比较，我现在去看看答案。

 

 

 

class Solution:

    def coinChange(self, coins: List[int], amount: int) -> int:

        dp = [0]*(amount+1)

        for i in range(1,amount+1):

            if i<min(coins):

                dp[i]=-1

                continue

            curmin = float(‘inf‘)

            for j in range(len(coins)):

                if i-coins[j]<0:continue

                if dp[i-coins[j]] == -1:continue

                curmin = min(curmin,dp[i-coins[j]]+1)

            dp[i] = curmin if curmin!=float(‘inf‘) else -1

        print(dp)

        return dp[-1]

 

如果动态规划，自底向上的方法都是这样的。