枚举算法的思想专题

Posted 2020-11-14 dgwblog

枚举算法的思想例题

 

solution0：

 

 

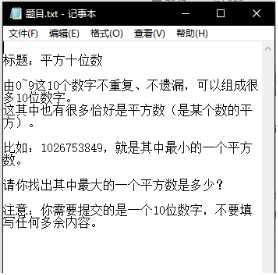
solution1：

思路1：由于要求最大值直接逆向枚举即可：最大的是9876543210，最小的是题目中给的1026753849。然后我们去判断是不是恰好包含0~9十个数字。再判断是不是完全平方数

 1 static void solution1(){
 2     Long i;
 3     for (i = 9876543210L; i > 1026753849; i--) {
 4         double q = (int)Math.sqrt(i*1.0);
 5         if(q*q==i){
 6             if(test(i)){
 7                 System.out.println(i);
 8                 break;
 9             }
10         }
11     }
12 }

View Code

 

 

思路2：枚举平方根，十位数的平方根，最小是30000，最大我们这里设的是100000，绰绰有余。然后我们根据Y算出X，这样X一定是完全平方数，我们也不用检查了。只用检查X是不是恰好十个数字：

 1 static void solution2(){
 2     for (int i=100000;i>30000;i--){
 3         long x= (long)i*i;
 4        // System.out.println(x);
 5         if(test(x)){
 6             System.out.println(x);
 7             break;
 8         }
 9     }
10 }

View Code

 

 

  判断是否重复的公共代码：

 

 1 private static boolean test(Long i) {
 2     Set<Integer> myset=new HashSet<>();
 3     long x=i;
 4     while (x!=0){
 5         int l = (int) (x % 10);
 6         myset.add(l);
 7         x/=10;
 8     }
 9     return  myset.size()==10;
10 }

View Code

 

 

 

总结：这个算法的复杂度就比之前的算法低了很多。枚举大概是10^5量级，判断是不是恰好十个数字还有O(10)的复杂度，总共大概是10^6量级。

 

solution2：

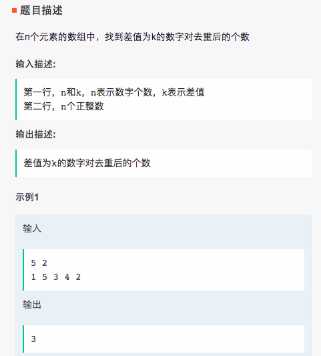
思路1： 一拿到题目不难看出，直接枚举数组的每一位，加上相应的差值，然后再次遍历数组看是否存在相应的值在这个数组中，然后处理重复即可得到答案，但是这个复杂度为O（N2），这里出现一个O（N）巧妙解法

 1  // O(N) example1
 2     static void solution2(){
 3         int n,k,ans=0;
 4         n=in.nextInt();
 5         k=in.nextInt();
 6         Set<Integer> myset =new HashSet<>();
 7         for(int i=0;i<n;i++){
 8             myset.add(in.nextInt());
 9         }
10         for(Integer x:myset){
11             if (myset.contains(x+k)){
12                 ans++;
13             }
14         }
15         System.out.println(ans);
16     }

 

 

solution3：

下面我们再看一道题，叫一面砖墙。这道题改编自网上Facebook去年的一道面试题，是hihoCoder的1494题（https://hihocoder.com/problemset/problem/1494）

 

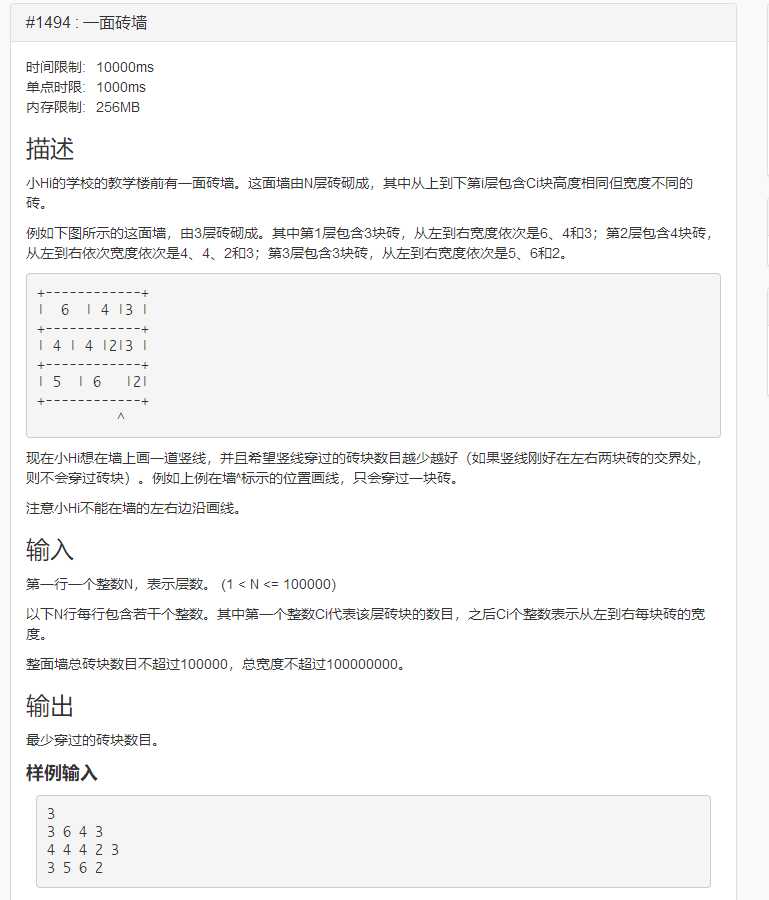
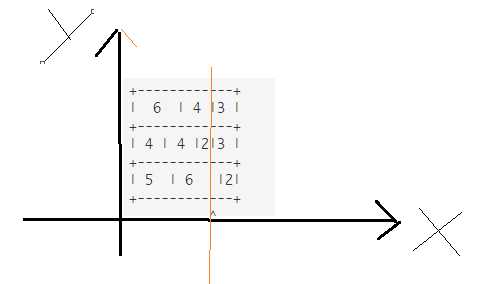
思路： 我拿到这个题目，直觉就是无法模拟出来，各个砖块之间好像又没有什么联系，但是仔细想一想 看下面的图，红色的线条即为 最优的穿墙答案，所以我们可以想到，在两块砖的缝隙处就是我们要找的答案，又可以发现

在砖块长度不一致的情况下 有宽度重合的地方，这个地方我们刚好可以用X坐标表示，那么在读入的时候，X坐标的重复的次数即为要，最终要穿透的位置。

 

 

 1 static void solution3(){
 2         int N;
 3         Map<Integer,Integer> mycoor=new HashMap<>();
 4         N=in.nextInt();
 5         for(int i=0;i<N;i++){
 6             int n,cnt=0;
 7             n=in.nextInt();
 8             for(int j=0;j<n;j++){
 9                 int xk=in.nextInt();
10                 cnt+=xk;
11                 Integer x1 = mycoor.get(cnt);
12                 if (x1==null) x1=0;
13                 if (j!=n-1)mycoor.put(cnt,++x1);
14                 System.out.println(x1);
15             }
16         }
17         int max=0;
18         for (Map.Entry<Integer,Integer> x:mycoor.entrySet()){
19               max=Math.max(x.getValue(),max);
20         }
21         System.out.println(N-max);
22     }

 

 

solution4：

 

 

 上面这道题目看似就是一道范围枚举题目，但是实际上需要完全的AC 需要注意的地方非常多，如果缩短时间复杂度 构造解析的等式的；

 一般做法就是枚举 这个等式 a^2+b^2+c^2+d^2=N 范围如下图，但是时间复杂度太高：【这里的/4 /3 /2 /1=再开放是为了 构造满足提议要求的递增规律】

 

所以可以分部分构造解： 把后一分部解提前构造出来：

 

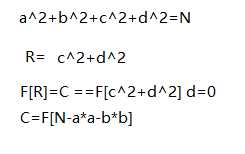
 1 static void solution1(){
 2         Map<Integer,Integer> f=new HashMap<>();
 3         int N=in.nextInt();
 4         //构造后部分解
 5         for(int c=0;c*c<=N/2;c++){
 6             for (int d=c;d*d+c*c<=N;d++){
 7                 if (!f.containsKey(d*d+c*c)){
 8                     f.put(c*c+d*d,c);
 9                 }
10             }
11         }
12         //构造前部分解
13         for (int a=0;a*a*4<=N;a++){
14             for (int b=a;b*b+a*a<=N/2;b++){
15                 if(f.containsKey(N-a*a-b*b)){
16                     Integer c = f.get(N - a * a - b * b);
17                     int d= (int) Math.sqrt((N-a*a-b*b-c*c)+1e-3);
18                     System.out.println(a+" "+b+" "+c+" "+d);
19                     return;
20                 }
21             }
22         }
23     }