XOR 的原理与应用

Posted 2021-03-07 yexuesong

理论

逻辑异或 - 维基百科

对于命题 (p, q)，(p) 异或 (q) 通常记作 (p XOR q) 或 (p oplus q)。在编程语言中，常写作 p ^ q。

阿贝尔群/交换群 - 维基百科

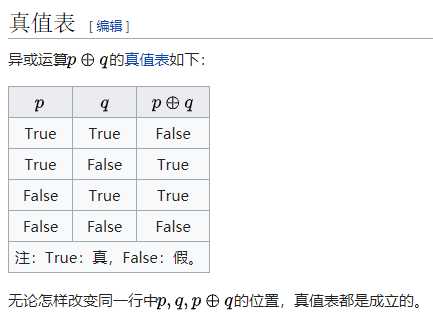
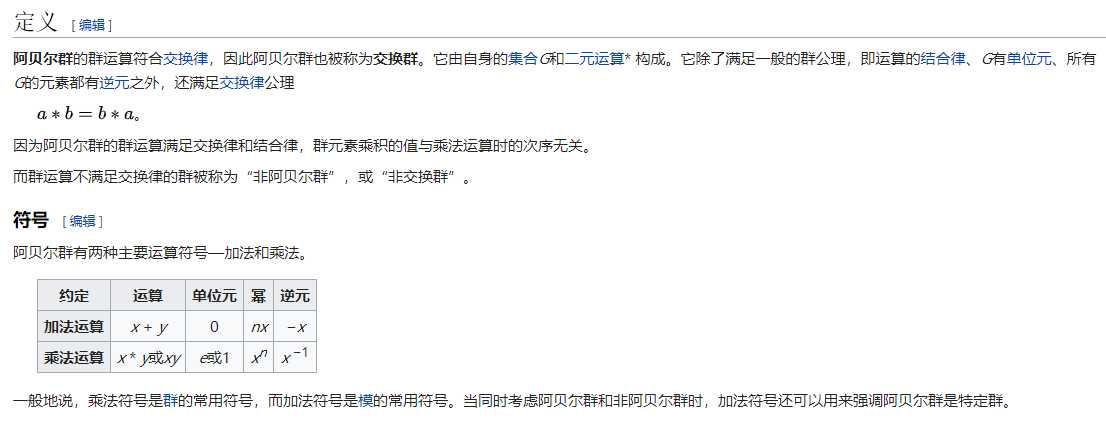
异或是 (mathbb{Z}_{2}) 群的加法运算，满足加法结合律和交换律。

应用

例一，利用其自反关系去交换 a, b 两个元素的值。

void swap(int *a, int *b)
{
    *a = *a ^ *b;
    *b = *a ^ *b;
    *a = *a ^ *b;
}

例如 a 为 101，b 为 011

第一次异或得到的是 110，其中 1 代表不同，0 代表相同

以第一次的结果作为「特征值」进行第二次异或，对 b 的每一位处理，特征为 1 则取反，特征为 0 则不变，即将 b 011 转换为 a 101

再用「特征值」对变成 a 的 b 进行异或，即可得到 b

例二，https://leetcode-cn.com/problems/missing-number/

给定一个包含 (0, 1, 2, cdots, n) 中 (n) 个数的序列，找出 (0 cdots n) 中没有出现在序列中的那个数。

int missingNumber(vector<int> &nums)
{
    int res = nums.size();
    for (int i = 0; i != nums.size(); ++i)
    {
        res ^= nums[i];
        res ^= i;
    }
    return res;
}