LightOJ - 1038（概率&DP）

Posted 2021-03-06 dialectics

题意：

　　给定一个数字N，每次可以用自身的因子来对自身进行分解，问将N分解为1所需分解次数的数学期望。

　　（给个数字Ｄ，我们可以选择1~Ｄ中可以被Ｄ整除的因子，除以D得到一个新的D，再用新D除以它的因子得到又一个新D，按次操作除到D=1时结束，求除的次数的期望值。）

解题思路：

　　定义：

　　D(N)：将N分解为1所需要的分解次数。

　　E(N)=E(D(N))：将N分解为1所需分解次数的数学期望。

 

　　对分解类型问题的首先想到能否对问题进行约归，即将问题转化成规模更小的问题，即考虑E（N）与E（X）（X<N）之间的关系。

　　设N的因子个数为cnt，分别记为a₁,a_2,a_3,……，第一次对N进行分解，可选的因子个数为cnt，且每个被选中的概率相等，又用一个因子a对N进行分解，N会变为另一个因子b（a*b=N），所以第一次对N进行分解后N会变为自身的某个因子，且变为每个因子的概率相等。

　　于是根据类似于全概率公式的思想：

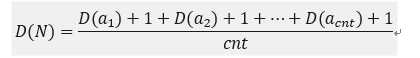　,设a_cnt=N；化简可得

　　

 

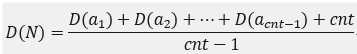
 　　再根据期望公式E（A+B）=E（A）+E(B）；

　　

 

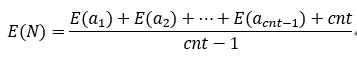
　　所以为求得E（N），我们先求得所有E（X）（X<N ）,然后再根据N的所有因子来计算E（N）。

 　　再考虑类似与筛法的思想，求的N的因子比较费事，但求的X是谁的因子非常简单，X是X*1，X*2，X*3....的因子。

　　所以我们可以按从小到达顺序，将E（a）的值加到它的倍数上，这样当遇到N的只需要(E（N）+cnt)/(cnt-1)就可以计算出E（N）。

　　N的cnt怎么计算，每有一个E（a）加到了N身上，N的cnt值就++。

核心思想：

　　变量分解，DP，筛法。

#include<iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;
const int MAXN=1e5+1;
double dp[MAXN];
int cnt[MAXN];
void pre(){
    for(int i=2;i<MAXN;i++){
        cnt[i]+=2;
        dp[i]+=cnt[i];
        dp[i]/=(cnt[i]-1);
        for(int j=2;i*j<MAXN;j++){
            dp[i*j]+=dp[i];
            cnt[i*j]++;
        }
    }
}
int main(){
    int T;
    scanf("%d",&T);
    int tmp;
    pre();
    for(int tt=1;tt<=T;tt++){
        scanf("%d",&tmp);
        printf("Case %d: %.7f
",tt,dp[tmp]);
    }
}

View Code