[计算机图形学]多边形扫描转换算法

Posted 2021-03-06 smallocean

多边形的表示

• 顶点表示。只要得到顶点再连线即可。如果是凸多边形由点集极角排序即可，其他情况不太了解
• 点阵表示。需要判断哪些属于内部点

本文主要讨论点阵表示

其实主要是PPT的copy，但是复制一遍确实印象深刻一点??

1.逐点判断法

即一个个点判断是不是属于图形内部，主要方法是射线法。

从待判断点发出射线，设与多边形交点个数为(k)

• (k)与多边形边的交点若为奇数，在内部；若为偶数，则该点在外部

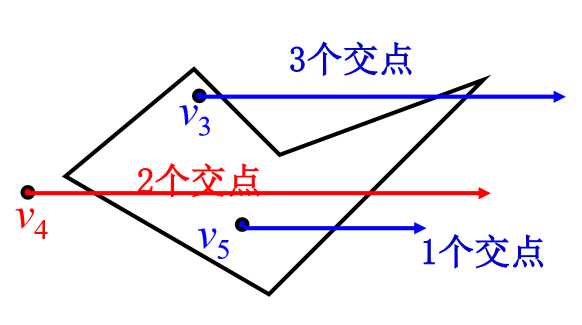
• 特殊情况：

  • 该点在边上，要先特判该点是不是边上一点
  • 射线在边上，会有无数个点，要特断射线是否与边同线
  • 交点为顶点，如果异测是1个，同侧算0个或2个

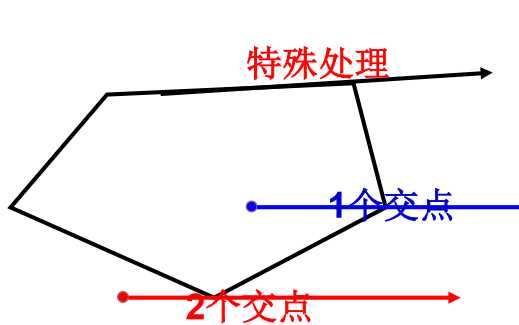
判断点的实现代码(ACM)：https://www.cnblogs.com/muyefeiwu/p/11260366.html

这个算法的特点是复杂度高

改进：利用内部点的连续性

2.扫描线算法

基本思路

• 扫描线一般取平行于(X)轴的直线，区间是指扫描线与边的交点
• 将扫描线与边的交点按(x)坐标从小到大排序
• 交点两两配对(交点个数为偶数),填充区间

连贯性

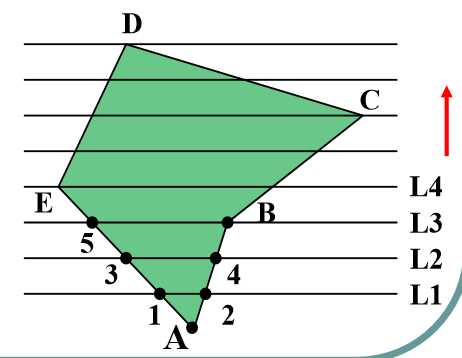
（1）边的连贯性(Edge Coherence)—优化交点计算

• 某条边与当前扫描线相交，也可能与下一条扫描线相交

• 如(L_1)与边AE和AB相交，下条扫描线(L_2)也与边AE和AB相交。

（2）扫描线的连贯性(Scan-line Coherence) )—优化交点排序

• 当前扫描线与各边的交点顺序与 下一条扫描线与各边的交点 顺序可能相同或类似

• 如点1,2的次序与点3,4的次序

（3）区间的连贯性(Span Coherence)

• 同一区间上的像素取同一颜色属性

• 如点3和点4之间的线段

交点计算

由扫描线(y＝e)与多边形的交点递推计算扫描线 (y＝e＋1)的交点

• 第一类交点：位于同一条边上的后继交点—如(I_0,I_2,I_4) : $x’＝x＋frac{1}{m} $

• 第二类交点：边与扫描线的第一个交点—如(I_3 , I_1) : 就是边的下端点

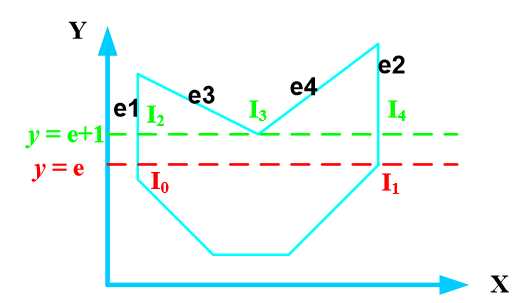
• 水平边不参与计算交点

算法数据结构

一、边的分类表(ET)(Edge Table)

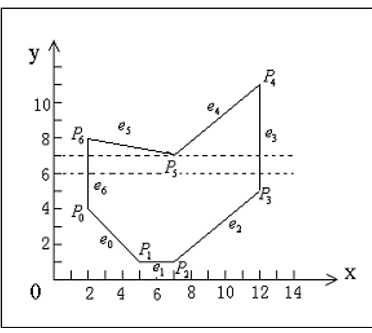
• 按照边的下端点，对非水平边进行分类的链表
• 下端点(y)坐标值等于(i)的边属于第i类，同类中有多条边时按(x)从小到大排序（(x)也一样时按边上端点的(x)值）

struct ET{
    int ymax;     //边的上端点的y坐标值
    float x;      //边的下端点的x坐标
    float deltax; //边的斜率的倒数
    ET *nextEdge; //下一条边的指针
}edga[N];         //每条扫描线对应一条链表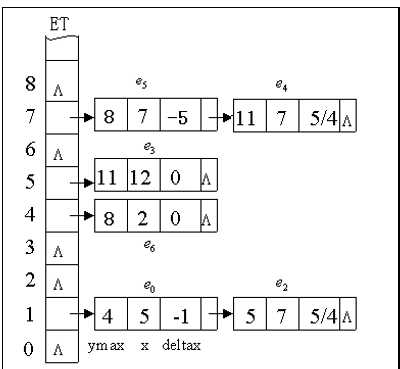

其中edga[0],edga[2],edga[3],edga[6],edga[8]因为没有与边的下端点相交，所以为空

数据结构对应相关方法：

• deltax：用于递推计算交点$x’＝x＋frac{1}{m} $
• ymax: 当扫描线 y = e + 1 == ymax，说明下 一条扫描线与此边不相交。

---

二、活性边表(AEL)(Active Edge List)

• 结构定义与(ET)表是一样的

• x的含义不一样：当前扫描线与边的交点的(x)坐标

• 作用：存储与当前扫描线的交点，同时快速计算下一条扫描线与多边形相交的点，且可判断边是否与下一条扫描线相交

• 实例

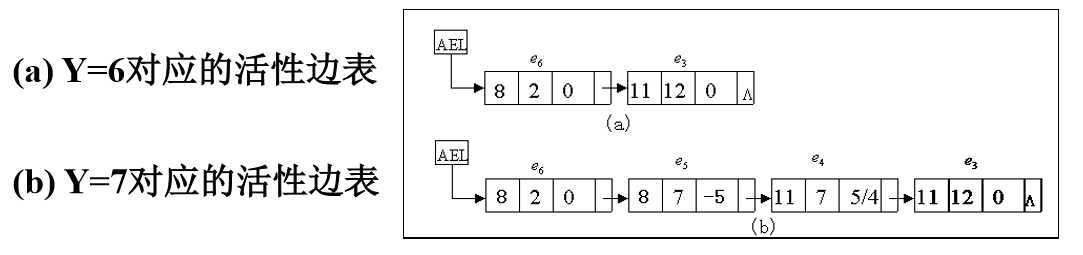
在(Y=7)的时候(ET)表不为空，所以就将(ET)表中的边插入到(AEL)表中

---

算法过程

• 先建立(ET)表，扫描线从下往上扫，即设置一个指针(p)，从(y_{min})开始
• 如果此时的(ET)表不为空，就将表中元素取出插入到(AEL)中，插入排序
• (AEL)表中的元素两两配对，获得填充区段，再填充
• p++
• 将(AEL)中满足(y = y_{max})边删去 因为每条边被看作下闭上开的
• 对(AEL)中剩下的每一条边的(x)递增(deltax)，即(x = x+deltax)
• 直到(ET)表和(AEL)表都为空，算法结束