Codeforces 1312D. Count the Arrays

Posted 2021-03-06 zxytxdy

Codeforces 1312D. Count the Arrays

题意：

计算满足如下要求的序列的数量。

• 1：序列长度为(n)。
• 2：序列中的元素为1~m。
• 3：序列中有且仅有一对数字相等。
• 4：序列有一个分界点，分界点左边的数字严格单调递增，右边的数字严格单调递减。

数据范围：(2leq nleq mleq 2e5)。

对结果取(mod 998244353)。

思路：

首先特判，就是当(n=2)时，没有满足条件的序列，输出0。

来看一般情况，为了方便理解，我们画一张图。

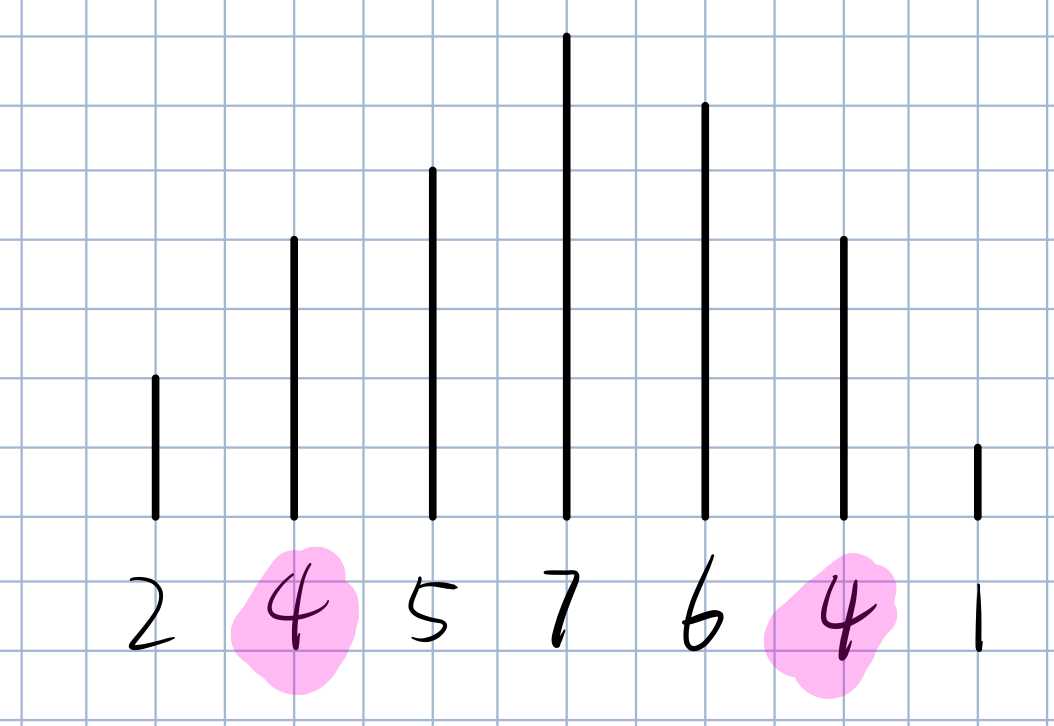
这是一个满足条件的序列，满足图像成山峰型，且仅一对数字相等。

我们可以发现，除了4相等之外，其他数字都是不同的。

所以我们可以转化一下。

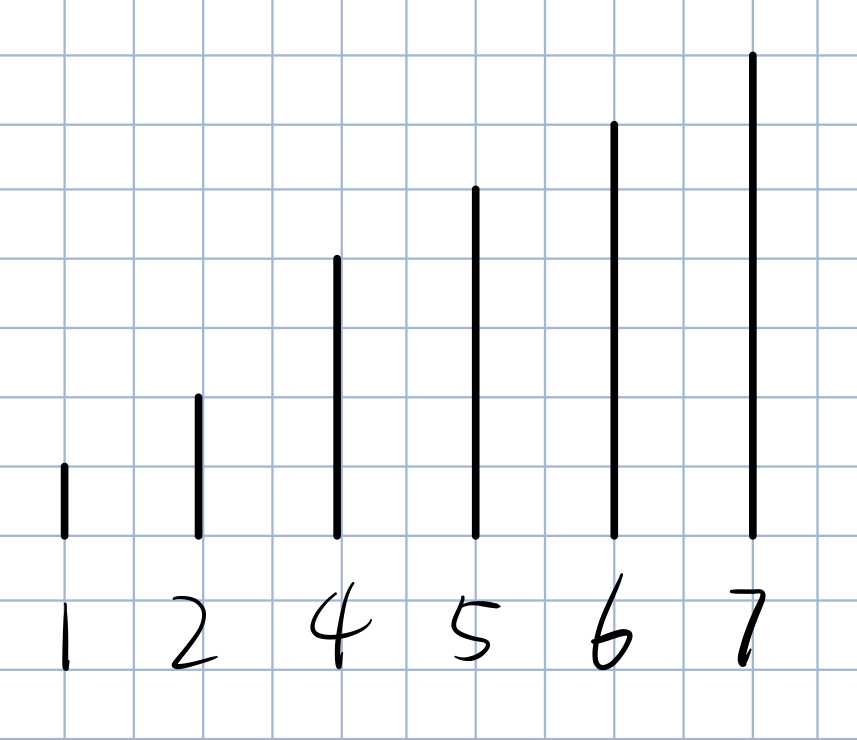
将其视为一个数字两两不同的递增序列，那满足这样条件的序列有多少种？

我们可以直接从(m)个数字中选(n-1)个出来，一定可以组成这样一个递增序列，所以答案是：
[ C_{m}^{n-1} ]
但是还有许多情况漏解，比如说我原序列有两个(1)，得到的递增序列也是如上图所示。

那么我们就会发现，除了最大的数字之外，所有的数字都可以裂化为两个放到最大数字的右边，所以此时我们要对答案乘上(n-2)。如图所示：

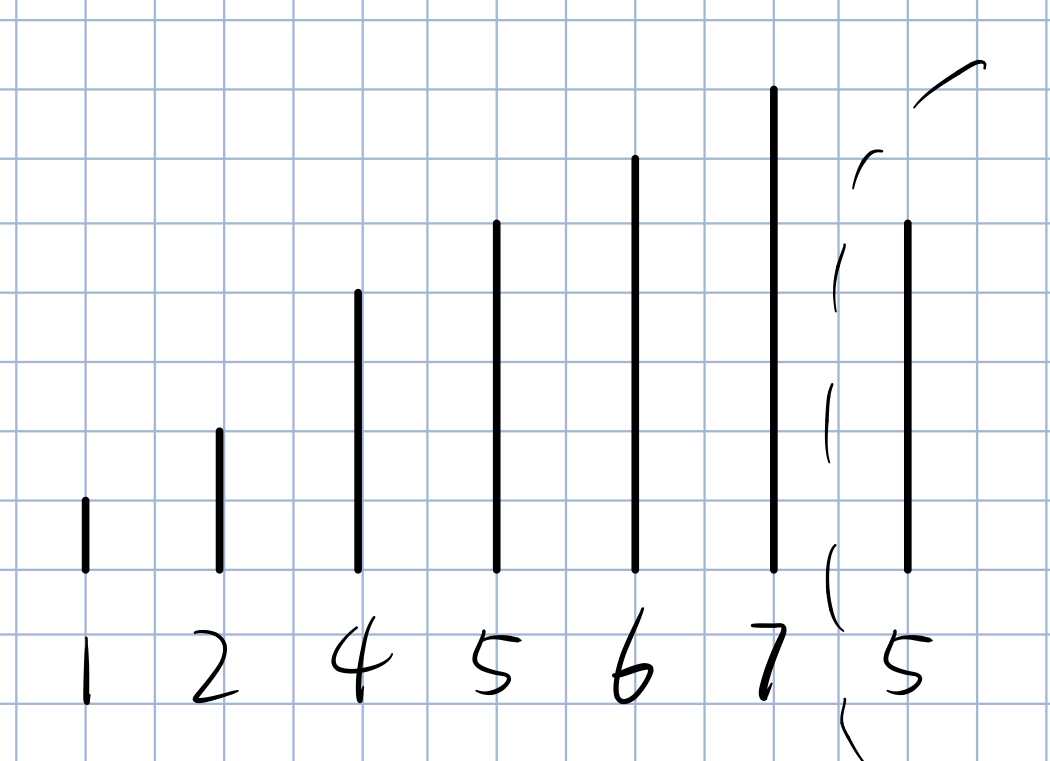
上图表示我们把一个5送到右边去。(1,2,4,5,6)都可以送到右边去。

此时还是会漏解，我们尝试把除了(5)之外的左边的数字移动到右边，那么有多少种方案？

首先在这(n-2)个数字当中，5不能右移过去，那也就是剩下(n-3)个数字，那么此时枚举往右放多少个数字，放(0,1,2,3,...,n-3)都是可以的，所以我们要对答案乘上：
[ C_{n-3}^0+C_{n-3}^1+C_{n-3}^2+...+C_{n-3}^{n-3}=2^{n-3} ]
综上所述，答案为：
[ C_m^{n-1} imes (n-2) imes 2^{n-3} ]
code