决策树详解
Posted tianyadream
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了决策树详解相关的知识,希望对你有一定的参考价值。
一、背景
网上有很多排序算法的总结,整理的一目了然,惹人喜爱,但关于决策树的相关博文,普遍存在以下问题
1)归纳程度不足,深度不够
2)总结点不足,有些疑问找不到答案
3)照抄现有书籍上的公式和推导过程
于是想到自己整理一篇关于决策树的文章,同时也加深自己的理解
二、正文
首先,不说话,直接上图
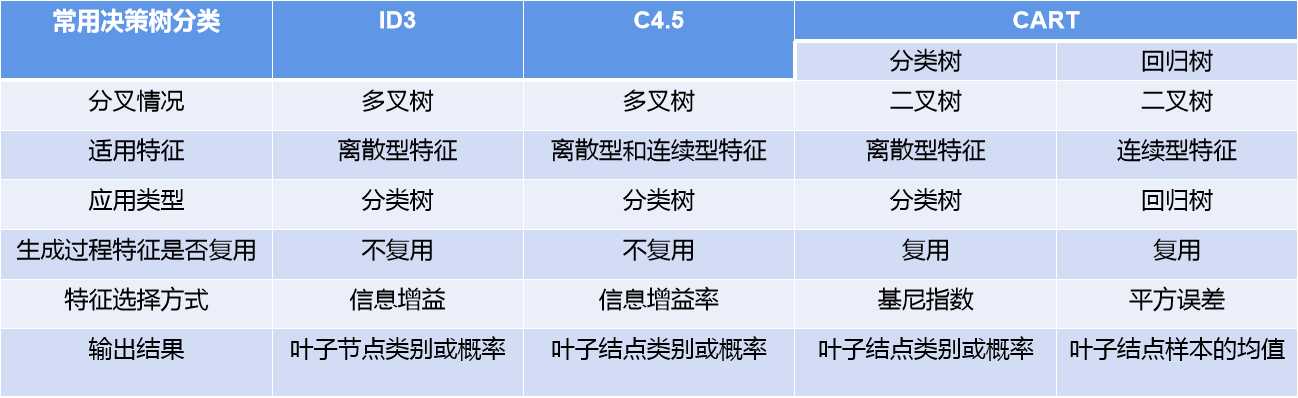
在解释上图之前,首先声明,本文尽可能避免公式的罗列(想看的可以翻书或者搜相关博文),尽量用自然语言(人话)去解释相关的概念。
要理解决策树之前,要理解如下几个概念:
1、概率,符号表示为p, p(x)代表随机事件x发生的概率,比如x代表天气情况,就有天气晴朗的概率和下雨的概率
2、信息量, 符号表示为h,h(x)代表随机事件x发生这件事包含多少信息量,h(x) = -logp(x),我们看到概率越小,信息量越大;举个例子,我们经常调侃某句话或者某张图的信息量有点大,在看这段话或这张图的时候你脑海中肯定闪过的是各种污污的小概率事件
3、熵,物理和化学中的概念,代表一个系统的混乱程度,熵越大,混乱程度越大,比如水蒸气的熵>水的熵>冰的熵
4、信息熵,符号表示为H, H(x)代表各种x所有可能取值的信息量的期望(可以粗糙地理解为信息量的平均值,实际为加权平均),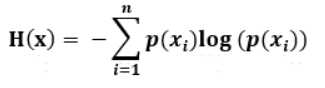 ,衡量事件x的确定程度,信息熵越大代表事件的可能性越多,越不确定,比如明天下雨和晴天的概率均为0.5,也就是不确定性最大的情况,这时信息熵为log2;当明天下雨的概率为1时,确定性最大,信息熵为0。
,衡量事件x的确定程度,信息熵越大代表事件的可能性越多,越不确定,比如明天下雨和晴天的概率均为0.5,也就是不确定性最大的情况,这时信息熵为log2;当明天下雨的概率为1时,确定性最大,信息熵为0。
5、条件熵,即为随机事件x发生的条件下y事件的信息熵的期望,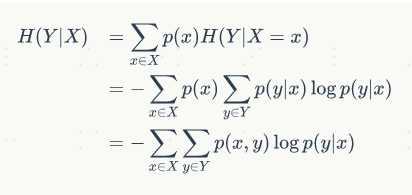 ,也即表示在已知随机变量X的条件下随机变量Y的不确定性的期望,强调的是随机事件x对随机事件y的不确定性的影响。比如随机事件y包括今天下雨或者晴天两种情况,随机事件x包括昨天晚上下雨或者晴天的两天情况;如果昨天晚上下雨,今天下雨的概率会增大,确定性会增加;如果昨晚晴天,今天晴天的概率会增加,确定性也会增加;所以考虑昨晚的天气情况x时,y的不确定性(条件熵)会减少。
,也即表示在已知随机变量X的条件下随机变量Y的不确定性的期望,强调的是随机事件x对随机事件y的不确定性的影响。比如随机事件y包括今天下雨或者晴天两种情况,随机事件x包括昨天晚上下雨或者晴天的两天情况;如果昨天晚上下雨,今天下雨的概率会增大,确定性会增加;如果昨晚晴天,今天晴天的概率会增加,确定性也会增加;所以考虑昨晚的天气情况x时,y的不确定性(条件熵)会减少。
6、信息增益(互信息)。随机变量y的信息熵减去考虑随机变量x的y的条件熵,即为信息增益;衡量在考虑随机变量x的情况下y的不确定性减少的程度。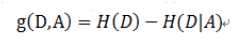
7、信息增益率。个人理解,信息增益率的存在意义在于弥补信息增益的应用缺陷。信息增益主要用于帮助选择某个能够减少目标变量不确定性的特征(随机变量),考虑极端情况,当选择唯一id这种随机变量时,会导致条件熵为0,信息增益最大,但这种情况没有任何泛化意义,所以需要对类似的情况进行惩罚,从而帮助我们做出更合理的选择。所以 信息增益率=信息增益/惩罚项,正好考虑到上述极端情况下我们选择的随机变量x的信息熵最大,所以惩罚项选择随机变量x的信息熵,最后公式为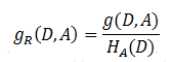
8、Gini(基尼)指数。从另一个角度衡量随机变量的不确定性。可以这样理解,随机事件x发生的概率为p,然后根据该概率对随机事件x进行预测,猜错的可能性为1-p,而对随机事件x的所有可能的猜错期望即为基尼指数。即系统越混乱越不确定,猜错的可能性的期望越高,基尼指数越高。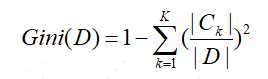 。
。
在详细说明每种决策树之前,我觉得有必要去理解一下决策树是什么:
1、编码角度,决策树是一系列if-else规则,他能通过一系列决策对样本进行处理并输出结果;它和硬编码一样可以做到对集合中样本的不重不漏地处理,而且通过学习算法得到决策树,相比人为硬编码不易出错,所以我觉得以后开发工程师的基本技术栈里不仅要包括数据结构与算法,还要包括机器学习。
2、概率论角度,决策树展示了目标变量y在给定特征条件下的条件概率分布。
在构造决策树的过程中,主要有三大步骤:
1、特征选择
2、决策树的生成(包含预剪枝)
3、决策树的剪枝(后剪枝)
下面我们分别针对三种常用的决策树进行介绍,他们分别为
1、ID3
2、C4.5
3、CART
2.1 ID3决策树
2.1.1 特征选择
应用场景:分类
依赖指标:信息熵、条件熵、信息增益
1、计算待分类样本的信息熵
2、计算某个特征条件下的条件熵
3、计算信息增益,选择最大信息增益对应的特征作为当前划分依据
4、对子节点,递归进行特征选择,待选择特征集去除了上一步已选择过的特征,即某个特征在从根到某个叶子结点的路径上不会重复出现
2.1.2 决策树的生成
输入:训练数据集D, 特征集A,阈值e,决策树的最大深度n,作为叶子结点要小于的样本数量m
输出:决策树T
1)若D中所有实例属于同一类,则T为单结点树,并将该类作为该结点的类标记,返回T
2)若A为空集,则T为单结点树,并将D中实例树最大的类作为该结点的类标记,返回T
3)否则,计算A中各特征对D的信息增益,选择信息增益最大的特征Ag
4)(预剪枝)如果Ag的信息增益小于阈值e,则置T为单结点树,并将D中实例树最大的类作为该结点的类标记,返回T
5)否则,对Ag的每一可能取值ai, 依Ag=ai将D分割为若干非空子集Di,将Di中实例树最大的类作为标记,构建子结点,由结点及其子结点构成树T, 返回T
6)对第i个子结点,以Di为训练集,以A-{Ag}为特征集,递归地调用(1)~(5)步,如果子结点的深度等于n或者子结点的样本数量小于m,则将该子结点作为叶子结点,停止递归调用,得到子树Ti,返回Ti
2.1.3 决策树的剪枝
决策树的生成是采用启发式算法(类似贪婪算法),每一步做出最优选择,实现的是局部最优,结果就是容易过拟合,因为模型记住了很多训练数据集特有的细节,这些细节会降低模型泛化的能力
决策树的剪枝采用的是最优化算法,明确整棵决策树(全局)的损失函数或代价函数(损失函数+结构风险正则化)进行迭代优化
代价函数如下:
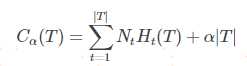
其中t代表某个叶子结点,Nt表示该叶子结点对应的样本数量,Ht表示该结点的经验熵(信息熵),|T|表示模型的复杂度,α控制正则化的强度
这里的Nt可以理解为权重,毕竟如果两个叶子结点的经验熵相同,包含子结点数量更多的那个结点对总体混乱程度的贡献更大。
输入:生成算法产生的决策树T,正则化参数α
输出:修剪后的子树Tα
1)计算每个结点的经验熵
2)递归地从树的叶节点向上回缩
3)如果回缩后的损失函数小于等于回缩前的,则进行剪枝
4)返回第二步调用,知道不能继续为止,得到剪枝后的决策树
2.2 C4.5决策树
C4.5树是基于ID3树的改进,具体表现为两点
1)特征选择使用信息增益率替代信息增益,具体原因请看文章开头关于信息增益和信息增益率的介绍(这一点很多资料都会讲到)
2)增加了对连续变量(特征)的支持(这一点很多资料没有讲,尤其是没有讲如何处理连续变量)
下面我们就讲一下C4.5决策树对特征的处理。
1)对于离散特征(分类或者顺序特征),该决策树采用N叉树的方式,对于每一个特征取值分出一个子结点,和ID3处理方式相同
2)对于连续型特征,采用二分法,
1、首先将样本按照该特征大小进行排序
2、每两个相邻特征值取平均值,将该平均值作为分裂点进行样本划分
3、计算每种划分所对应的信息增益,选取信息增益最大的分裂点作为最终二分的分裂点
4、计算所有特征的信息增益率,选取信息增益率最大的特征作为当前划分依据
3)划分后的样本不再保留其原有值,而用布尔值代替。
这里有两个问题需要解释:
Q1:为什么连续特征的最佳分裂点选取使用信息增益而非信息增益率?
我的理解是,因为同一个特征下,最终的结果确定是二分,这种相对的比较,也就不存在信息增益自身的缺陷(倾向于选择情况更少的特征,现在情况只有两种)
Q2:为什么最佳特征的选择标准为信息增益率而非信息增益?
因为离散特征多种取值会对应N种划分,而连续特征只会是二分,如果用信息增益,则倾向于选择连续型特征(情况更少,只有两种)
2.3 CART树(分类树)
2.3.1 特征选择
使用最小化基尼指数,具体来讲,
1)对所有特征的所有可能切分点进行基尼指数计算
2)选择基尼指数最小的特征+切分点组合
2.3.2 决策树的生成
输入:训练数据集D,停止计算的条件(预剪枝条件,参考ID3决策树)
输出:CART决策树
根据训练数据集,从根节点开始,递归地对每个结点进行以下操作:
1)设结点的训练数据集为D,计算现有特征对该数据集的基尼指数。此时,对每一个特征A,对其可能取的每个值a(对于大量连续变量计算代价过高,可以选择分类发生变化的点),根据样本点对A=a的测试为‘是’或‘否’,将D分割成D1和D2两部分![]() ,根据
,根据![]() 计算A=a时的基尼指数。
计算A=a时的基尼指数。
2)在所有可能的特征A以及他们所有可能的切分点a中,选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点。依最优特征与最优切分点,从现结点生成两个子结点,将训练数据集依特征分配到两个子结点中去。
3)对两个子结点递归地调用(1)(2),直至满足停止条件
4)生成决策树
2.3.3 决策树的剪枝
CART的剪枝这里不详细讲解了,总体而言就两个过程
1)根据生成的完整决策树,计算每个内部结点对应的损失函数增加量,然后砍去损失函数增加最多的结点,生成新树
2)对新树递归调用第一步,生成更多的新树,构成树集合
3)通过验证集选择最佳的决策树
上图

注意第六步中应该返回步骤3,这是一个错误。该图片摘自李航的《统计学习方法》
2.4 CART树(回归树)
2.4.1 特征选择
根据平方误差最小化准则
1)对每个特征进行排序,依次选择不同的切分点对样本进行切分
2)计算切分后子结点中样本的值与与样本均值的平方误差和,选择平方误差和最小的切分点和左右子结点平方误差和最小的特征
3)对子结点递归进行1、2步
2.4.2 决策树生成

2.4.3 决策树的剪枝
和CART(分类树)的剪枝几乎相同,不同点在于损失函数由基尼指数变为了最小二乘。
3、补充
1、关于决策树的具体输出结果问题
A:拿skleran关于决策树的API来讲,对于分类树,既可以用predict()方法直接获得分类的结果,也可以用predict_prob()获得样本属于某个类别的概率
2、关于整个预测流程是怎样的?
A:首先通过训练数据集训练出了决策树,包括决策树的结构和结点,且根据训练样本分配到每个叶子结点的数量计算出了每个叶子结点对应的所属类别的概率(好多资料只提到了叶子结点对应了该节点所属类别最多的样本对应的类别)。然后待预测样本只需要根据所训练出的决策树走到决策树的某个叶子结点,输出该结点早就计算好的分类类别或者某个类别的概率即可(回归树则输出该结点对应训练样本的平均值)。
Finished!
感觉还是没有做到通俗易懂啊。。。little sad
参考资料:
1、李航-统计学习方法
2、葫芦娃-百面机器学习
以上是关于决策树详解的主要内容,如果未能解决你的问题,请参考以下文章