字符串匹配算法

Posted 2021-03-06 dazhu123

1：简单匹配算法

算法思路：

• 先在源字符串S中第一个位置开始匹配，依次与目标字符串T的字符进行判断。
• 如果遇到到不同，则退出本次匹配，再将S中匹配起始位置+1，然后重复。
• 直到T的字符全部匹配完毕，则认为找到一个字符串。

算法流程：

1. 初始化字符串和起始位置 i = 0;j = 0
2. S字符串循环
   1. 在循环判断T字符串上字符和S上字符的相等是否
      1. 若相等，则i++，j++，若j已经超过S的长度则认为已经匹配完成直接return，否则继续循环匹配
      2. 若不等，则break本次T字符循环。
3. 如果上述循环结束，直接return false；

代码示例：

    public int index2(String S,String T,int pos){
        int i = pos;
        int j = 0;
        int temp = 0;
        for(;i<=S.length()-T.length();i++){
            //保存此次匹配的搜索起始地址
            //以被，重新搜索
            temp = i;
            for(;j<T.length();){
                if(S.charAt(temp)==T.charAt(j)){
                    temp++;
                    j++;
                    //如T字符串已经全部搜索完毕
                    if(j == T.length()){
                        return i;
                    }
                }
                else{
                    j=0;
                    break;
                }
            }
        }
        //如果上面循环，还没有找到的话，就return 0 表示没有匹配
        return 0;

    }

2：KMP模式匹配算法

　　上面简单的匹配算法，理解方便。但是在计算机系统中，字符都是由大量的01和数组组成，这种大量的重复的机构会十分的低效。

举个例子：S字符串为

String S = "000000000000000000000000000001";
String D = "00001";

由于S和D的最后一字符为1，其他为0，所以每次在S的循环判断，都在在进行到D的最后一位失效。而这种情况判断则所有的S的循环，十分的低效。

　　KMP算法的关键是求出next数组，next数组中存放的是当目标数组该位置与源数组不同时，通过next数组找到下一个index的位置的辅助数组。

我们以000001为例子。

 

 

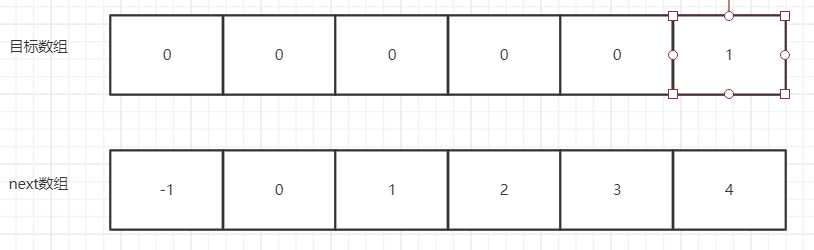
1. next[0] = -1 代表当目标数组[0]不匹配时，将移动源字符串。
2. next[1] = 0 代表当目标数组[1]不匹配时，将在目标数组[0]处重新判断。
3. next[2] = 1 代表当目标数组[2]不匹配时，将在目标数组[1]处重新判断。
4. 。。。。。。

　　上面的操作的原因；是目标数组中存在前缀和后缀重复的部分字符串，这字符串在当前位置字符不匹配之前，就已经判断过了。所以可以跳过这部分字符串进行匹配。假如没有重复的字符串则还是要从头开始在匹配的!

2.1讲解getNext方法

    public  int[] getNext(String ps) {
        char[] p = ps.toCharArray();
        int[] next = new int[p.length];
        next[0] = -1;//初始化条件；next[0] = -1意味着如果目标字符第0个字符就不匹配，则源字符串移位。
        int j = 0;//j初始化为0，从0开始进行构建next数组
        int k = -1;
        //下面是通过递归的思想，我们上面已经有初始条件了，
        //然后假设已经有了next[j]如何求next[j+1]尼？
        //分两种情况；
        // 情况1：p[j] = p[k],其中k = next[j]的，即上面假设已经有next[l]的情况下，则因为k = next[j],p[j] = p[k]
        //则有next[j+1] = k+1 = next[j]+1;因为在p[j]和p[k]之前已经有了重复字符串，所以该情况下只需要加一即可！
        //情况2：p[j] ！= p[k]，因为p[j] ！= p[k]，所以k和j前面的重复字符分别加上p[j]和p[k]不可能构成重复数组，但是由于
        //已经有next[j] = k，所以也会有next[k] = k1，则我们可知在k1前面和k的前面也存在重复字符。而k的前面和j的前面存在重复字符。，所以在看
        //由于p[j] ！= p[k]，我们把目标放在p[j] == p[k1]？一旦出现相等，则p[j+1]也求出来了！即next[j+1] = k1+1;
        //如果不相等，则不断重复直到k = -1，代表没有相等，则赋值成-1+1 = 0;
        //该求法；使用的使递归的思想，有初始条件，然后通过next[j]来求next[j+1]。不断计算完整个next的过程。
        while (j < p.length - 1) {
            if (k == -1 || p[j] == p[k]) {
                next[++j] = ++k;
            } else {
                k = next[k];
            }
        }
        return next;
    }