堆排序

Posted 2021-03-06 wyd-blogs

　　堆排序是一种树形选择排序，特点：L[1...n]视为一颗完全二叉树的顺序存储结构，利用完全二叉树中双亲与孩子节点的内在关系，在当前无序区中选择关键字（最大或最小）元素。

　　大顶堆：L(i)>L(2i) && L(i)>L(2I+1)　　

　　小顶堆：L(i)<L(2i) && L(i)<L(2I+1)

例：

 

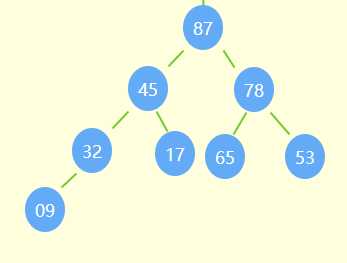
• 堆的初始化
  • 大顶堆

　　　　　　对所有具有双亲结点含义编号从大到小（ n/2 ~1）做出如下调整：

　　　　　　1）若孩子结点皆小于双亲结点，则该结点的调整结束

　　　　　　2）若存在孩子结点大于双亲结点，则将最大的孩子结点与双亲结点交换，并对该孩子结点进行1）、2），直到出现1）或到叶节点为止 

　　　　　　

//建立大堆
void BuildMAxHeap(int a[], int len)
{
    for(int i=len/2; i>0; i--)
        AdjustDown(a, i, len);
}
//将元素向下调整
void AdjustDown(int a[], int k, int len)
{
    a[0]=a[k];
    for(int i=2*k; i<=len; i*=2)
    {
        if(i<len && a[i]<a[i+1])
            i++;
        if(a[0]>=a[i])
            break;
        else
            a[k] = a[i];
        k = i;
    }
    a[k]=a[0];
}

初始化

• 堆排序

　　不断地输出堆顶元素，并向下调整

 

void HeapSort(int a[], int len)
{
    BuildMAxHeap(a,len);
    for(int i=len; i>1; i--)
    {
        swap(&a[i], &a[1]);
        AdjustDown(a, 1, i-1);;
    }
}

排序

 

• 堆插入

　　将新结点放置在末端然后进行向上调整

void HeapSort(int a[], int len)
{
    BuildMAxHeap(a,len);
    for(int i=len; i>1; i--)
    {
        swap(&a[i], &a[1]);
        AdjustDown(a, 1, i-1);;
    }
}

向上调整