POJ3735——mat乘法优化

Posted 2021-03-05 mingusu

题目链接：http://poj.org/problem?id=3735

题目意思：有n只猫，有三种操作得花生，吃花生，换花生。k种操作，进行m轮

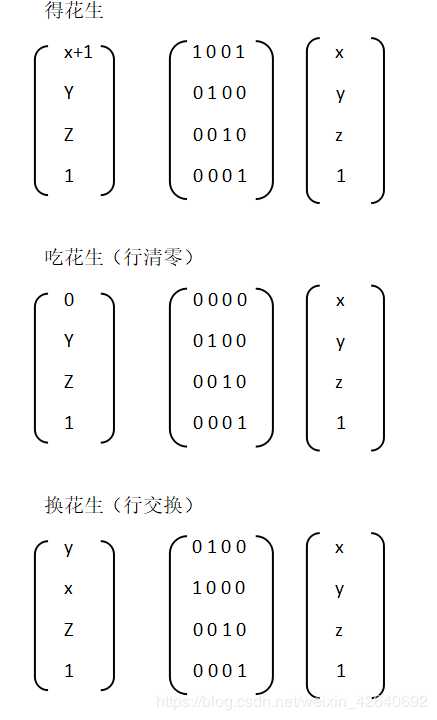
解题思路：m很大，考虑矩阵变化，考虑每一个变化过程，由于有加一，将初始矩阵末尾增加一，方便进行操作，然后有如下网上借鉴（chaoxi）来的变换。

要注意的是：题意很简单但是因为理解错题意，以为重复m次是每进行一次操作就重复，但是正确的理解是全部操作整体进行m次重复，由于m的数据较大，所以用矩阵快速幂，用矩阵快速幂的时候必须进行优化（因为是稀疏矩阵矩阵），否则会超时。

1 for(i=1;i<=n;++i)
2   for(j=1;j<=m;++j)
3     for(l=1;l<=k;++l)
4       c[i][l]+=a[i][j]*b[j][l];

参考博客：

mat乘法优化：https://blog.csdn.net/gogdizzy/article/details/9003369

Glacier-elk的博客：https://www.cnblogs.com/Glacier-elk/p/9489655.html

还有一件事：在做矩阵乘法的时候，最好是按照我上面代码的循环顺序计算，因为如果你改变了循环顺序，速度就会变慢，如果你不相信的话可以去试一试，这是因为按照我代码的顺序，在计算一部分值之前，他的原值已经存在缓存中了，这样的话是比从内存中读取快的，而改变顺序的话，就会从内存中调用，就会变慢了。如果还不理解：可以这样考虑，这份代码将j循环移动到了中间，最内层变成了l循环，这个代码的意义在于：在最内层循环，对于c和b的访问都是顺序的了，而这个循环中a[i][k]不变，这样就更好的利用了cpu cache。矩阵越大，这个加速效果越明显。

 

#include<iostream>
#include<string.h>
#include<algorithm>
typedef long long ll;
using namespace std;
const int maxn = 110;
ll t,n,m,k;
struct matrix
{
    ll a[maxn][maxn];
    matrix()
    {
        memset(a,0,sizeof(a));
    }
    friend matrix operator * (matrix x,matrix y)
    {
        matrix ans;
        for(int i = 1;i <= n+1;i++)
        {
            for(int j = 1;j <= n+1;j++)
            {
                if(x.a[i][j])
                for(int k = 1;k <= n+1;k++)
                    ans.a[i][k] += (x.a[i][j]*y.a[j][k]);
            }
        }
        return ans;
    }
    friend matrix operator ^ (matrix x,ll k)
    {
        matrix unit;
        memset(unit.a,0,sizeof(unit.a));
        for(int i = 1;i <= n+1;i++) unit.a[i][i] = 1;
        while(k)
        {
            if(k&1) unit = unit * x;
            x = x * x;
            k >>= 1;
        } 
        return unit;
    }
};
int main()
{
    while(~scanf("%lld%lld%lld",&n,&m,&k))
    {
        if(!n&&!m&&!k) return 0;
        matrix res,ans;
        memset(ans.a,0,sizeof(ans.a));
        memset(res.a,0,sizeof(res.a));
        for(int i = 1;i <= n+1;i++) res.a[i][i] = 1;
        ans.a[n+1][1] = 1;
        for(int i = 1;i <= k;i++)
        {
            char ch;
            int b,c;
            getchar();
            scanf("%c",&ch);
            if(ch == ‘g‘) 
            {
                scanf("%d",&b);
                res.a[b][n+1]++;
            }
            else if(ch == ‘e‘)
            {
                scanf("%d",&b);
                for(int j = 1;j <= n+1; j++) res.a[b][j] = 0;
            }
            else if(ch == ‘s‘)
            {
                scanf("%d%d",&b,&c);
                for(int j = 1;j <= n+1;j++) swap(res.a[b][j],res.a[c][j]); 
            }
        }
        res = res ^ m;
        /*
        for(int i = 1;i <= n+1;i++)
        {
            for(int j = 1;j <= n+1;j++)
            printf("%lld ",res.a[i][j]);
            printf("
");
        }
        */
        ans = res * ans;
        for(int i = 1;i <= n;i++)
        {
            if(i == 1)
            printf("%lld",ans.a[i][1]);
            else printf(" %lld",ans.a[i][1]);
        }
        printf("
");
    }
    return 0;
}