排序总结

Posted 2021-03-05 coderyang1

1.冒泡排序

• 思想：

  • 两个数比较大小，较大的数下沉，较小的数冒起来。

  • 过程：

    • 比较相邻的两个数据，如果第二个数小，就交换位置。
    • 从后向前两两比较，一直到比较最前两个数据。最终最小数被交换到起始的位置，这样第一个最小数的位置就排好了。
    • 继续重复上述过程，依次将第2.3...n-1个最小数排好位置。

　　时间复杂度:O(n2)

代码：

 1 public static void BubbleSort(int [] arr){
 2 
 3      int temp;//临时变量
 4      for(int i=0; i<arr.length-1; i++){   //表示趟数，一共arr.length-1次。
 5          for(int j=arr.length-1; j>i; j--){
 6 
 7              if(arr[j] < arr[j-1]){
 8                  temp = arr[j];
 9                  arr[j] = arr[j-1];
10                  arr[j-1] = temp;
11              }
12          }
13      }
14  }

优化：

• 针对问题：
  数据的顺序排好之后，冒泡算法仍然会继续进行下一轮的比较，直到arr.length-1次，后面的比较没有意义的。

• 方案：
  设置标志位flag，如果发生了交换flag设置为true；如果没有交换就设置为false。
  这样当一轮比较结束后如果flag仍为false，即：这一轮没有发生交换，说明数据的顺序已经排好，没有必要继续进行下去。

 1 public static void BubbleSort1(int [] arr){
 2 
 3    int temp;//临时变量
 4    boolean flag;//是否交换的标志
 5    for(int i=0; i<arr.length-1; i++){   //表示趟数，一共 arr.length-1 次
 6 
 7        // 每次遍历标志位都要先置为false，才能判断后面的元素是否发生了交换
 8        flag = false;
 9        
10        for(int j=arr.length-1; j>i; j--){ //选出该趟排序的最大值往后移动
11 
12            if(arr[j] < arr[j-1]){
13                temp = arr[j];
14                arr[j] = arr[j-1];
15                arr[j-1] = temp;
16                flag = true;    //只要有发生了交换，flag就置为true
17            }
18        }
19        // 判断标志位是否为false，如果为false，说明后面的元素已经有序，就直接return
20        if(!flag) break;
21    }
22 }

 

2.简单选择排序

• 思想：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对 n个元素进行排序总共进行至多 n-1次交换

 

 

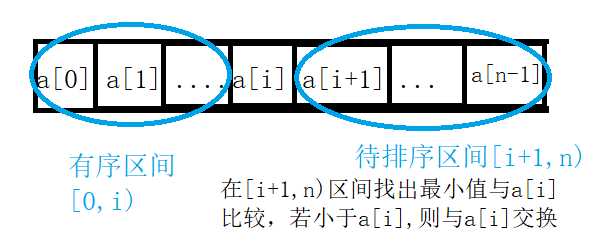
• 时间复杂度：O（n*n）
• 代码

 

 1 /*
 2     * 简单选择排序
 3     * */
 4     public static void selectSort(int a[],int n){
 5 //有序区间[0,i) 无序区间[i,n)
 6         for (int i=0;i<n-1;i++){//遍历n-1次
 7             int k=i;//最小值下标
 8             for(int j=i+1;j<n;j++){ //从[i+1,n)区间找出最小值和a[i]比较
 9                 if (a[j]<a[k]){
10                     k=j;
11                 }
12             }
13             if (a[i]!=a[k]){//最小值和a[i]交换
14                 int temp=a[i];
15                 a[i]=a[k];
16                 a[k]=temp;
17             }
18 
19         }
20     }

3.希尔排序

基本思想：
在要排序的一组数中，根据某一增量分为若干子序列，并对子序列分别进行插入排序。
然后逐渐将增量减小,并重复上述过程。直至增量为1,此时数据序列基本有序,最后进行插入排序。

时间复杂度：O(n1.5)

 1 public static void shell_sort(int array[],int lenth){
 2 
 3    int temp = 0;
 4    int incre = lenth;
 5 
 6    while(true){
 7        incre = incre/2;
 8 
 9        for(int k = 0;k<incre;k++){    //根据增量分为若干子序列
10 
11            for(int i=k+incre;i<lenth;i+=incre){
12 
13                for(int j=i;j>k;j-=incre){
14                    if(array[j]<array[j-incre]){
15                        temp = array[j-incre];
16                        array[j-incre] = array[j];
17                        array[j] = temp;
18                    }else{
19                        break;
20                    }
21                }
22            }
23        }
24 
25        if(incre == 1){
26            break;
27        }
28    }
29 }

 

4. 插入排序

• 思想：在待排序的一组数据中，假定前n-1个数有序，将第n个数插入到前面的有序序列中，使得这n个数也保持有序，具体做法是从后往前枚举已有序序列，进行比较，确定插入位置

 

 

 

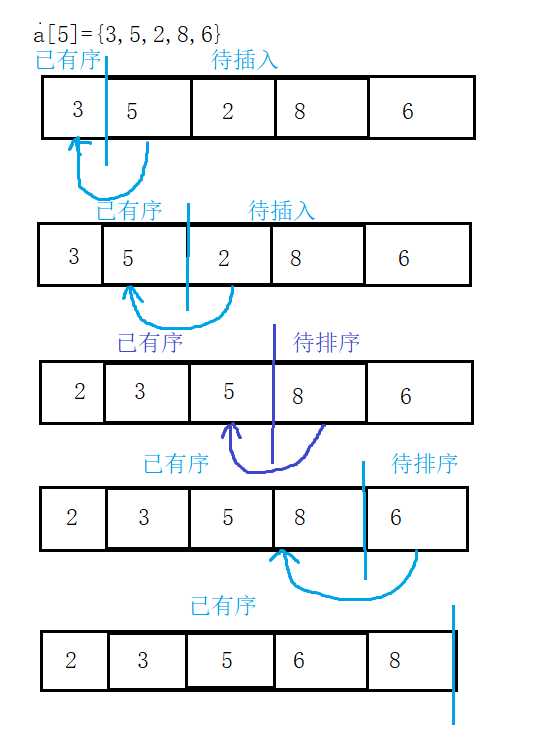
• 时间复杂度：O（n*n）

代码：

 1  /*
 2     * 插入排序
 3     * */
 4     public static void insertSort(int a[]){
 5         for (int i=0;i<a.length-1;i++){
 6             for (int j=i+1;j>0;j--){
 7                 if (a[j]<a[j-1]){
 8                     int temp=a[j];
 9                     a[j]=a[j-1];
10                     a[j-1]=temp;
11                 }
12                 else break;
13             }
14         }
15     }

5.快速排序：

• 思路：分治思想，复杂度：O(N*logN)
  • 先从数列中取出一个数作为基准值；
  • 将比这个数小的数全部放在它的左边，大于或等于它的数全部放在它的右边；
  • 对左右两个小数列重复第二步，直至各区间只有1个数。

代码：

/*
    * 快速排序
    * */
    //划分区间对【left，right】进行划分
    public static int partition(int []a,int left,int right){
        int temp=a[left];//a[left]存放至临时变量
        while (left<right){//只要left和right不相遇
            while (left<right&&a[right]>=temp) right--;//反复左移right
                a[left]=a[right];
            while (left<right&&a[left]<temp) left++;//反复右移left
                a[right]=a[left];
        }
        a[left]=temp;//把temp放到left和right相遇的地方
        return left;
    }
    public static void quickSort(int a[],int left,int right){
        if (left>=right){//当前区间长度不超过1
            return;
        }
            int pos=partition(a,left,right);//将[left,right]按a[left]一分为二
            quickSort(a,left,pos-1);//对左子区间递归进行快速排序
            quickSort(a,pos+1,right);//对右子区间进行快速排序
    }

6.归并排序

• 思路：2-路归并排序，其原理是，将序列两两分组，将序列归并为【n/2】个组，组内单独排序；然后将这些组在两两归并，生成【n/4】个组，组内再单独排序；以此类推，直到只剩下一个组为止
• 时间复杂度：O(nlogn)
• 例子:将序列{66,12,33,57,64,27,18} 进行2-路归并排序

1. 第一趟。两两分组，得到四组：{66,12}、{33,57}、{64,27}、{18}，组内单独排序，得到新序列{{12,66}，{33,57}，{27,64}，{18}}
2. 第二趟。将四个组继续两两分组，得到两组：{12,66,33,57}，{27,64,18}，组内单独排序，得到新序列{{12,33,57,66}，{18,27,64}}
3. 第三趟。将两个组继续两两分组，得到一组：{12,66,33,57,27,64,18}，组内单独排序，得到新序列{12,18,27,33,57,64,66}

整个过程如下图：

 

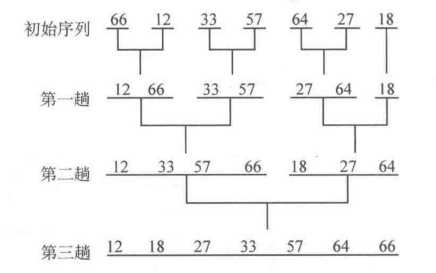
2-路归并排序的核心在于如何将两个有序序列合并为一个有序序列

代码：

 

 1 /*
 2     * 归并排序
 3     * */
 4     public static void merge(int A[],int L1,int R1,int L2,int R2){
 5         /*将[L1,R1][L2,R2]合并为有序区间，L2=R1+1*/
 6         int maxn=100;
 7         int i=L1,j=L2;
 8         int [] temp=new int[maxn];//temp 临时数组存放合并后的数组，index为其下标
 9         int index=0;
10         while(i<=R1&&j<=R2){
11             if (A[i]<=A[j]){
12                 temp[index++]=A[i++];//将A[i]加入序列temp
13             }else{
14                 temp[index++]=A[j++];//将A[j]加入序列temp
15             }
16         }
17         while(i<=R1) temp[index++]=A[i++];//将[L1,R1]的剩余元素加入序列temp
18         while(j<=R2) temp[index++]=A[j++];//将[L2,R2]的剩余元素加入序列temp
19         for (i=0;i<index;i++){
20             A[L1+i]=temp[i];//将合并后的序列赋值回数组A
21         }
22     }
23     public static void mergeSort(int A[],int left,int right){
24         if (left<right){
25             int mid=(left+right)/2;//取【left，right】的中点
26             mergeSort(A,left,mid);//递归将左子区间【left，mid】归并排序
27             mergeSort(A,mid+1,right);//递归将右子区间【mid+1，right】归并排序
28             merge(A,left,mid,mid+1,right);//将左子区间和右子区间合并
29         }
30     }