直方图中的最大矩形

Posted 2021-03-05 hhyx

# 题意

直方图是在公共基线处对齐的一系列矩形组成的多边形，各矩形具有相同的宽度，但可以有不同的高度，求最大矩形的面积
例如

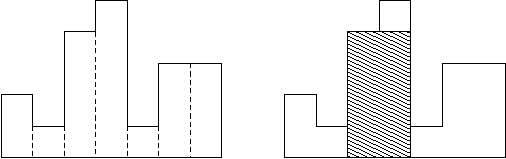
阴影部分即最大面积

# 题解
建立一个递增单调栈，保存高度
1） 当前矩形的高度比栈顶矩形高，直接进栈
2） 当前小于栈顶就不断去除，累计所有取出的矩形的宽度之和，并且每弹出一个矩形，就用他的高度呈上累计的宽度更新答案，过程结束后再将当前矩形入栈，增加一个高度为0的矩形，避免栈中有剩余矩形

 1 #include<bits/stdc++.h>
 2 #define ll long long
 3 using namespace std;
 4 const int N = 1e5+10;
 5 int n;
 6 int a[N],stk[N];
 7 int wid[N];
 8 void work(){
 9    memset(stk,0,sizeof stk);
10    for(int i = 1; i <= n; i++)
11       cin >> a[i];
12    a[n+1] = 0;
13    int idx = 0;
14    ll ans = 0;
15    for(int i = 1; i <= n + 1; i++){
16       if(a[i] > stk[idx]){
17          stk[++idx] = a[i];
18          wid[idx] = 1;
19       }
20       else{
21          int width=0;
22          while(stk[idx] > a[i]){
23             width += wid[idx];
24             ans=max(ans,(ll)stk[idx]*width);
25             idx--;
26          }
27          stk[++idx] = a[i];
28          wid[idx] = width + 1;
29       }
30    }
31    cout << ans << endl;
32 }
33 int main(){
34    ios::sync_with_stdio(0);
35    cin.tie(0);
36    cout.tie(0);
37    while(cin >> n && n){
38       work();
39    }
40 }