能量项链(区间DP入门)

Posted 2021-03-05 iss-ue

题面:能量项链https://www.luogu.com.cn/problem/P1063

---

 

乍一看和石子合并差不多，可是多了头值和尾值，看起来十分麻烦

我们画一张图，紫色表示头值，蓝色表示尾值。规定西边那个珠子编号为1，然后顺时针编号

 

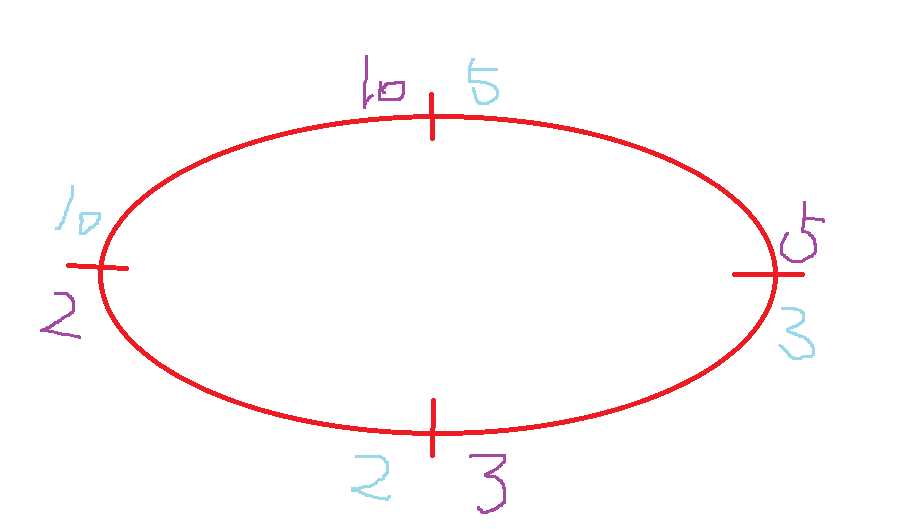
 很明显，我们现在要解决的是 dp [ i ] [ k ] 和 dp [ k+1 ] [ j ] 合并成的 dp [ i ] [ j ] 会变成什么样子

考虑1珠子和2珠子如果已经合并在一起，我们发现合并后的头值是1珠子的头值，合并后的尾值是2珠子的尾值

那么，是不是说dp [ i ] [  k ] 的头值就是a [ i ] ,尾值就是 a [ k+1 ] 呢

那么，是不是说 dp [ k+1 ] [ j ] 的头值就是a [ k+1 ],尾值就是 a [ j+1 ] 呢

状态转移方程就为:dp [ i ] [ j ] = max ( dp [ i ] [ j ] , dp [ i ] [ k ] + dp [ k+1 ] [ j ] + a [ i ] * a [ k+1 ] * a [ j+1 ] );

然后因为是环形，所以要扩大一倍计算。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m;
ll a[209],dp[209][209];
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)    cin>>a[i];
    for(int i=n+1;i<=n*2;i++)
        a[i]=a[i-n];
    for(int l=2;l<=n;l++)
    {
        for(int i=1;i+l-1<=2*n;i++)
        {
            int j=i+l-1;
            for(int k=i;k<=j-1;k++)
            {
                dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+a[i]*a[k+1]*a[j+1]);
            //    dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+a[i-1]*a[k]*a[j]);
            }
        }
    }
    ll ans=0;
    for(int i=1;i<=n+1;i++)
        ans=max(ans,dp[i][i+n-1]);
    cout<<ans;
}