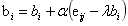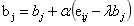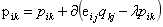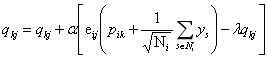SVD++分解

Posted 2021-03-05 little-horse

　　在现实情况下，用户的显式反馈严重不足，但一般拥有大量隐式反馈信息。所以在偏置svd基础上增加了用户的隐式反馈信息，该方法融合了用户的显式和隐式信息。

1.预测评分公式为

　　 

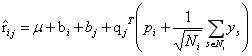
　　其中，有全局平均分，user的偏置信息，item的偏置信息，N_i为该用户评价过的所有item集合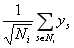，从隐式反馈出发，作为用户偏好的补充，y_s为隐式偏好。

2.损失函数为平方误差+L2正则项，其中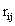是真实评分。

 　　

 3.利用SGD训练更新，其中。

• 
•  
•  
•  
•  

 4.程序，(数据movielens 100k，https://github.com/jiangnanboy/recommendation_methods/blob/master/com/sy/reco/recommendation/matrix_factorization/svdpp.py)

import numpy as np
import math

‘‘‘
融合了BiasLFM以及用户的隐式行为
‘‘‘
class SVDPP():
    ‘‘‘
    初始化ratingMatrix,F, alpha, λ
    ratingMatrix:评分矩阵
    F:隐因子数目
    alpha:学习速率
    λ:正则化参数，以防过拟合
    ‘‘‘
    def __init__(self, ratingMatrix, F, alpha, λ):
        self.ratingMatrix = ratingMatrix
        self.F = F
        self.alpha = alpha
        self.λ = λ

    # 对U,I,Y矩阵初始化，随机填充，根据经验随机数与1/sqrt(F)成正比,bu向量与bi向量初始化为全0,u是所有有评分的全局平均
    def __initPQ(self, userSum, itemSum):
        self.U = np.zeros((userSum, self.F))
        self.I = np.zeros((itemSum, self.F))
        self.Y=np.zeros((itemSum,self.F))
        self.bu = np.zeros(userSum)
        self.bi = np.zeros(itemSum)
        self.meanV = np.mean(self.ratingMatrix[self.ratingMatrix > 0])  # 全局均值
        for i in range(userSum):
            self.U[i] = [np.random.random() / math.sqrt(self.F) for x in range(self.F)]
        for i in range(itemSum):
            self.I[i] = [np.random.random() / math.sqrt(self.F) for x in range(self.F)]
            self.Y[i]=[np.random.random()/math.sqrt(self.F) for x in range(self.F)]

    # 迭代训练分解，max_iter:迭代次数
    def iteration_train(self, max_iter):
        userSum = len(self.ratingMatrix)  # 用户个数
        itemSum = len(self.ratingMatrix[0])  # 项目个数
        self.__initPQ(userSum, itemSum)  # 初始化U,I,Y,bu,bi
        Z=np.zeros((userSum,self.F))
        for step in range(max_iter):
            for user in range(userSum):
                Z[user]=self.U[user]
                ru=1/math.sqrt(len(self.U[user][self.U[user,:]>0]))#1/sqrt(Usum>0)用户评过分的项目个数
                for item in range(itemSum):
                    if self.ratingMatrix[user, item] > 0:  # 未评分的项目不参与计算
                        for f in range(self.F):
                            Z[user,f]+=self.Y[item,f]*ru #I更新中的部分(1/sqrt(Usum))*self.Y
                sum=np.zeros(self.F)
                for item in range(itemSum):
                    if self.ratingMatrix[user,item]>0:# 未评分的项目不参与计算
                        eui = self.ratingMatrix[user, item] - self.predict(user, item,ru)  # 真实值减去预测的值
                        self.bu[user] += self.alpha * (eui - self.λ * self.bu[user])  # 更新bu
                        self.bi[item] += self.alpha * (eui - self.λ * self.bi[item])  # 更新bi
                        for f in range(self.F):
                            sum[f]+=self.I[item,f]*eui*ru #Y更新中的部分eui*ru*I
                            self.U[user, f] += self.alpha * (self.I[item, f] * eui - self.λ * self.U[user, f])  # 更新U
                            self.I[item,f]+=self.alpha*(eui*(self.U[user,f]+Z[user,f])-self.λ*self.I[item,f])#更新I
                #更新Y
                for item in range(itemSum):
                    for f in range(self.F):
                        self.Y[item,f]+=self.alpha*(sum[f]-self.λ*self.Y[item,f])
            #self.alpha*=0.9

        predictRating = []#存放全部预测数据
        for user in range(userSum):
            userItemRating = []
            ru = 1 / math.sqrt(len(self.U[user][self.U[user, :] > 0]))  # 1/sqrt(Usum>0)用户评过分的项目个数
            for item in range(itemSum):
                pui = self.predict(user, item,ru)
                userItemRating.append(pui)
            predictRating.append(userItemRating)
        return np.round(np.array(predictRating), 0)

    #预测打分，用户的行与项目的列
    def predict(self,user,item,ru):
        z=np.zeros(self.F)
        for i in range(len(self.ratingMatrix[user])):
            if self.ratingMatrix[user,i]>0:
                for f in range(self.F):
                    z[f]+=self.Y[i,f]
        pui =0.
        for f in range(self.F):
            pui+=(self.U[user,f]+z[f]/ru)*self.I[item,f]
        pui+=self.meanV+self.bu[user]+self.bi[item]
        return pui

    # 预测误差训练，convergence:误差收敛，小于这个误差,则终止训练
    def convergence_train(self, convergence):
        userSum = len(self.ratingMatrix)  # 用户个数
        itemSum = len(self.ratingMatrix[0])  # 项目个数
        self.__initPQ(userSum, itemSum)  # 初始化U,I,Y,bu,bi
        Z = np.zeros((userSum, self.F))
        flag=True
        while flag:
            for user in range(userSum):
                Z[user] = self.U[user]
                ru = 1 / math.sqrt(len(self.U[user][self.U[user, :] > 0]))  # 1/sqrt(Usum>0)用户评过分的项目个数
                for item in range(itemSum):
                    if self.ratingMatrix[user, item] > 0:  # 未评分的项目不参与计算
                        for f in range(self.F):
                            Z[user, f] += self.Y[item, f] * ru  # I更新中的部分(1/sqrt(Usum))*self.Y
                sum = np.zeros(self.F)
                for item in range(itemSum):
                    if self.ratingMatrix[user, item] > 0:  # 未评分的项目不参与计算
                        eui = self.ratingMatrix[user, item] - self.predict(user, item, ru)  # 真实值减去预测的值
                        self.bu[user] += self.alpha * (eui - self.λ * self.bu[user])  # 更新bu
                        self.bi[item] += self.alpha * (eui - self.λ * self.bi[item])  # 更新bi
                        for f in range(self.F):
                            sum[f] += self.I[item, f] * eui * ru  # Y更新中的部分eui*ru*I
                            self.U[user, f] += self.alpha * (self.I[item, f] * eui - self.λ * self.U[user, f])  # 更新U
                            self.I[item, f] += self.alpha * (
                            eui * (self.U[user, f] + Z[user, f]) - self.λ * self.I[item, f])  # 更新I
                # 更新Y
                for item in range(itemSum):
                    for f in range(self.F):
                        self.Y[item, f] += self.alpha * (sum[f] - self.λ * self.Y[item, f])

            cost = 0  # 误差
            for user in range(userSum):
                ru = 1 / math.sqrt(len(self.U[user][self.U[user, :] > 0]))  # 1/sqrt(Usum>0)用户评过分的项目个数
                for item in range(itemSum):
                    if self.ratingMatrix[user, item] > 0:
                        cost += (1 / 2) * math.pow(self.ratingMatrix[user, item] - self.predict(user, item,ru), 2)
                        cost += (1 / 2) * self.λ * (math.pow(self.bu[user], 2) + math.pow(self.bi[item], 2))
                        for f in range(self.F):
                            cost += (1 / 2) * self.λ * (math.pow(self.U[user, f], 2) + math.pow(self.I[item, f], 2)+math.pow(self.Y[item,f],2))
            if cost < convergence:
                flag = False

        predictRating = []  # 存放全部预测数据
        for user in range(userSum):
            userItemRating = []
            ru = 1 / math.sqrt(len(self.U[user][self.U[user, :] > 0]))  # 1/sqrt(Usum>0)用户评过分的项目个数
            for item in range(itemSum):
                pui = self.predict(user, item, ru)
                userItemRating.append(pui)
            predictRating.append(userItemRating)
        return np.round(np.array(predictRating), 0)