进阶实验6-3.2 社交网络图中结点的“重要性”计算 (30分)-dijkstra算法

Posted 2021-03-04 snzhong

 

 

 

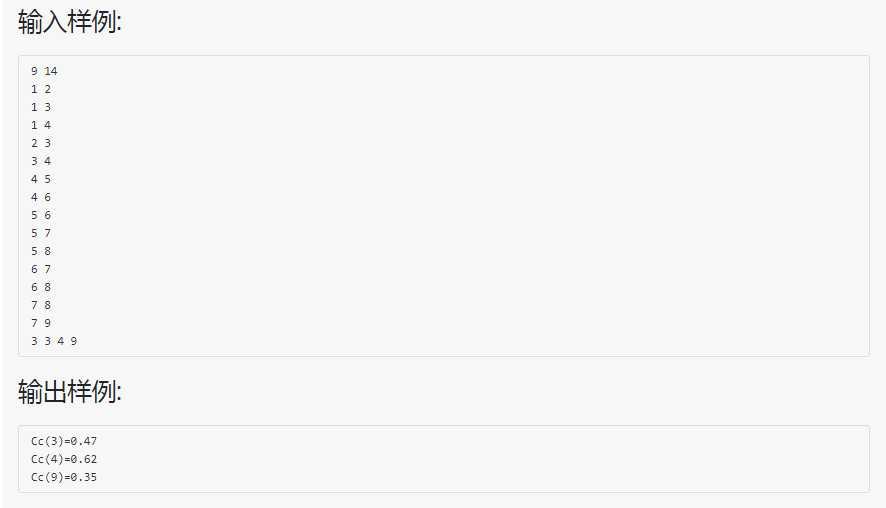
 解题思路：（邻接矩阵存储）

用dijkstra算法依次求出每个结点到其余结点的最短距离

#include <stdio.h>
#include <string.h>
#define INF 0x3f3f3f3f
#define MaxVex 1000+10
int G[MaxVex][MaxVex];
int visit[MaxVex];
int Nv,Ne;
void Init() {
    memset(G,INF,sizeof(G));
    int i;
    for(i=1; i<=Nv; i++) {
        G[i][i]=0;
    }
    int v1,v2;
    for(i=0; i<Ne; i++) {
        scanf("%d %d",&v1,&v2);
        G[v1][v2]=1;
        G[v2][v1]=G[v1][v2];
    }
}
void Dijkstra(int s) {
    visit[s]=1;
    int i,j,w,MIN;
    for(j=1; j<=Nv; j++) {
        MIN=INF;
        for(i=1; i<=Nv; i++) {
            if(!visit[i]&&G[s][i]<MIN) {
                MIN=G[s][i];
                w=i;
            }
        }
        visit[w]=1;
        for(i=1; i<=Nv; i++) {
            if(!visit[i]&&MIN+G[w][i]<G[s][i]) {
                G[s][i]=MIN+G[w][i];
            }
        }
    }
}
int main() {
    scanf("%d %d",&Nv,&Ne);
    Init();
    int i,j;
    for(i=1; i<=Nv; i++) {
        memset(visit,0,sizeof(visit));
        Dijkstra(i);
    }
    int sum[MaxVex]={0};
    for(i=1; i<=Nv; i++) {
        for(j=1; j<=Nv; j++)
            sum[i]+=G[i][j];
    }
    int n,x;
    scanf("%d",&n);
    for(i=0; i<n; i++) {
        scanf("%d",&x);
        float tmp=(float)(Nv-1)/(float)sum[x];
        printf("Cc(%d)=%.2f
",x,tmp);
    }
    return 0;
}