2D到3D 外参矩阵估计

Posted 2021-03-04 xiaochun-zhao

1. 背景

最近正在做姿态估计，简单搜姿态估计的关键字得到的信息不够完整，所以把搜到的信息加上自己的理解整合在这篇文章。

2. 正向3D到2D的过程

先上一张图【已经自带水印就偷懒省下引用】：

 

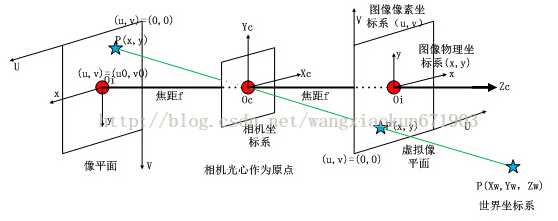
首先3D物体在世界坐标系，也就是我们现实世界，物体是现实中的绝对尺寸，以m为单位。现实世界的物体认为成刚体，那么这个刚体和相机之间会有一个相对位置。对于物体来说，是以自身的中心为原点，需要把自身的尺寸映射到以相机光心为原点的相机坐标系。也就是对物体的绝对坐标做一些平移和旋转，变换坐标的圆心和轴向。

 

 

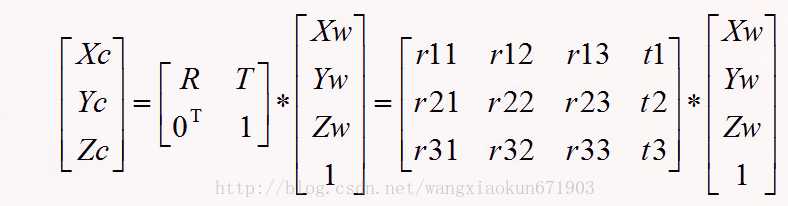
物体经过镜头（透镜）在焦距位置成像，也就是图中最左边的像平面。这个像平面是以o1-xy为坐标系的。根据透镜成像原理，这个成像和实际物体相比是倒像，然而我们希望得到的图片是正像，所以就在对称位置取了虚拟像平面，这个就是图像坐标系。在图像坐标系中图片的尺寸大小是和感光元件（Sensor Size）相关的，以mm为单位。通常在相机说明书里以 μm 为单位给出，例如：Image Area：5856 μm x 3276 μm。看上图的右半部分，相机坐标系的物体平面和图像坐标系与相机光心形成金字塔结构，所以可以利用相似性得出变化坐标。下图中的（Xc，Yc，Zc）是指物体在相机坐标系中的坐标。

 

 

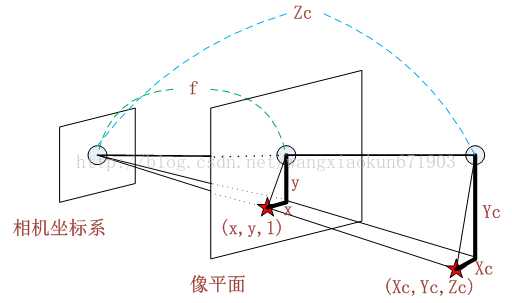
 由图就很容易得出：

 

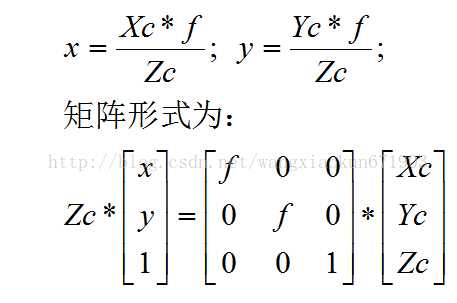
 像素坐标系是指可视化后图片的坐标系，也叫是通常左上角为原点，向右向下为正方向的坐标系。在图像坐标系还需要变换到像素坐标系才能得到我们看得到的图片。像素是离散化的点，而成像是连续的，因此从图像坐标系到像素坐标系的转换也叫离散化。在不考虑畸变和仿设的情况下，变换公式如下：

 

 （u,v）是像素坐标系坐标，（x,y）是图像坐标系坐标。dx和dy是计算出来的像素大小。

 

整个转换过程如下：

 

图像物理转像素坐标系和相机坐标系到图像物理坐标系的复合就是相机的内参矩阵，而世界坐标系到相机坐标系的转换就是内参矩阵。

 3. 2D到3D姿态估计

这个问题定义是：在有2D特征点的情况下找到3D旋转的外参矩阵，也就是找到上图中的世界坐标系到相机坐标系的变换矩阵。很显然，我们需要知道内参矩阵，像素2D坐标和3D世界坐标才能求解外参矩阵。内参矩阵可以使用相机标定或者说明书参数估计方法。相机标定用棋盘格的方法很多博客教程，就不在这里重述，主要写一下根据给定数据估算的方法【1】：

假设摄像头的焦距为4mm,像片的尺寸大小为640x480，传感器尺寸为5856 μm x 3276 μm，像素大小为3μm x 3μm。即f=4， dx = 640/5.856, dy=480/3.276。u0 = 640/2， v0 = 480/2。从而内参矩阵可以直接代入参数得出。

以头部姿态估计为例，3D世界坐标就是给出实际物理模型（3DMM）的3D特征点，对应的2D特征点可以通过很多算法获得。之后可以通过solvePnp的方法求解外参矩阵。

 

参考：

【1】由相机的自身参数求解内参矩阵