进阶实验6-3.3 天梯地图 (30分)-Dijkstra

Posted 2021-03-04 snzhong

 

 

 

 

 

 

 

 

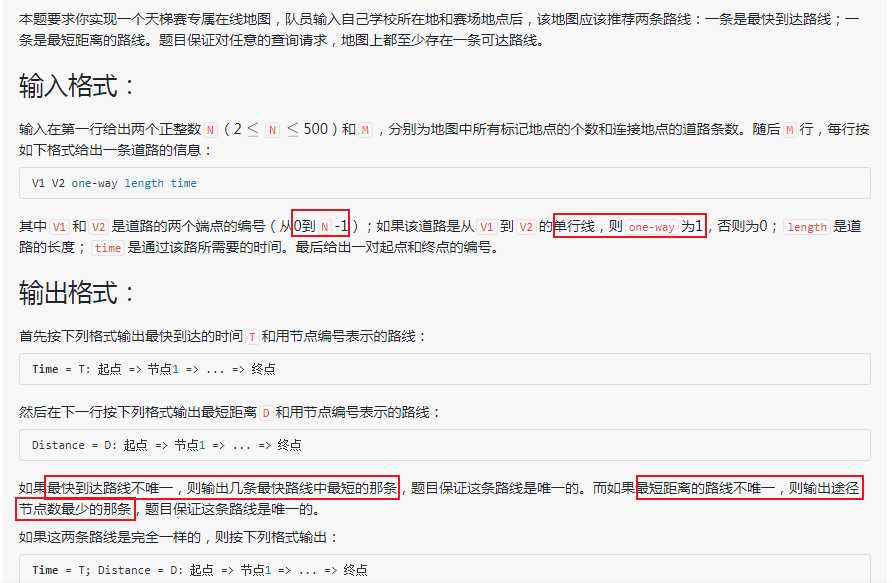
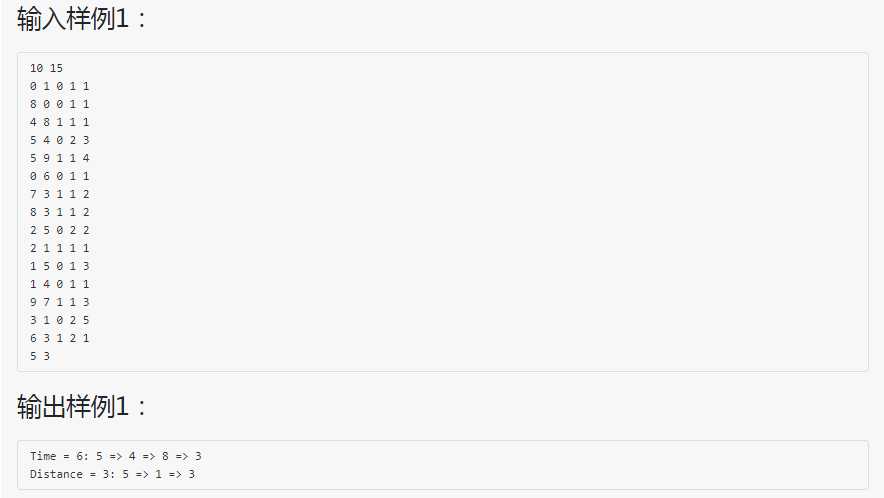
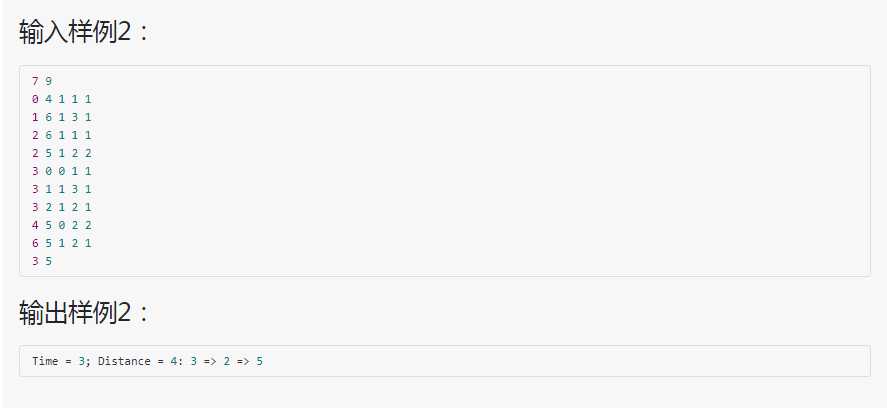
 解题思路：采用Dijkstra算法，算两次，一次算最短时间，一次算最短路径，另开一数组记录路径

#include <stdio.h>
#include <string.h>
#define INF 0x3f3f3f3f
#define MaxVex 500
typedef struct {
    int length;
    int time;
} Graph;
Graph G[MaxVex][MaxVex];//图 
int visit[MaxVex]= {0};//访问标记 
int fpath[MaxVex];//最快路径 
int lpath[MaxVex];//最短路径 
int num[MaxVex]={0};//节点计数 
int Nv,Ne;
//图初始化-邻接矩阵 
void Init() {
    int i,j;
    for(i=0; i<Nv; i++) {
        for(j=0; j<Nv; j++) {
            G[i][j].length=INF;
            G[i][j].time=INF;
        }

    }
    int v1,v2,one_way,length,time;
    for(i=0; i<Ne; i++) {
        scanf("%d %d %d %d %d",&v1,&v2,&one_way,&length,&time);
        G[v1][v2].length=length;
        G[v1][v2].time=time;
        if(!one_way) {
            G[v2][v1]=G[v1][v2];
        }
    }
}
void Dijkstra(int s,int type) {
    visit[s]=1;
    num[s]=1;
    int i,j,w,MIN;
    //计算最快路径，如果最快路径不唯一，则选最短路径 
    if(type==1) { 
        for(i=0; i<Nv; i++) {
            MIN=INF;
            for(j=0; j<Nv; j++) {
                if(!visit[j]&&G[s][j].time<MIN) {
                    MIN=G[s][j].time;
                    w=j;
                }
            }
            visit[w]=1;
            for(j=0; j<Nv; j++) {
                if(!visit[j]&&MIN+G[w][j].time<G[s][j].time) {
                    G[s][j].time=MIN+G[w][j].time;
                    fpath[j]=w;
                } else if(!visit[j]&&MIN+G[w][j].time==G[s][j].time) {
                    //注意这里的最短路径是 G[w][j].length<G[fpath[j]][j].length
                    //而不是G[s][w].length+G[w][j].length<G[s][j].length 
                    if(G[w][j].length<G[fpath[j]][j].length) {
                        fpath[j]=w;
                    }
                }
            }
        }
    } else if(type==2) {//计算最短路径，如果不唯一，则先节点少的 
        for(j=0; j<Nv; j++) {
            MIN=INF;
            for(i=0; i<Nv; i++) {
                if(!visit[i]&&G[s][i].length<MIN) {
                    MIN=G[s][i].length;
                    w=i;
                }
            }
            visit[w]=1;
            for(i=0; i<Nv; i++) {
                if(!visit[i]&&MIN+G[w][i].length<G[s][i].length) {
                    G[s][i].length=MIN+G[w][i].length;
                    lpath[i]=w;
                    num[i]=num[w]+1;
                } else if(!visit[i]&&MIN+G[w][i].length==G[s][i].length) {
                    if(num[w]+1<num[i])
                    {
                        num[i]=num[w]+1;
                        lpath[i]=w;
                    
                    }
                    
                }
            }
        }
    }
}
//判断两条路径是不否一样 
int IsTheSame(int a[],int n,int b[],int m) {
    if(n!=m)
        return 0;
    else {
        int i;
        for(i=0; i<=n; i++) {
            if(a[i]!=b[i])
                return 0;
        }
        return 1;
    }
    
}
int main() {
    scanf("%d %d",&Nv,&Ne);
    Init();
    int s,d,i;
    scanf("%d %d",&s,&d);
    memset(visit,0,sizeof(visit));
    for(i=0; i<Nv; i++) {
        fpath[i]=s;
    }
    Dijkstra(s,1);

    memset(visit,0,sizeof(visit));
    for(i=0; i<Nv; i++) {
        lpath[i]=s;
    }
    Dijkstra(s,2);
    //逆向输出路径存入数组 
    int f=d,l=d;
    int FRoad[MaxVex]= {0},LRoad[MaxVex]= {0};
    int t=0,k=0;
    while(f!=s) {
        FRoad[t++]=f;
        f=fpath[f];
    }
    FRoad[t]=s;
    while(l!=s) {
        LRoad[k++]=l;
        l=lpath[l];
    }
    LRoad[k]=s;
    //结果输出 
    if(IsTheSame(FRoad,t,LRoad,k)) {
        printf("Time = %d; Distance = %d: ",G[s][d].time,G[s][d].length);
        for(i=t; i>=0; i--) {
            printf("%d",FRoad[i]);
            if(i)
                printf(" => ");
        }
    } else {
        printf("Time = %d: ",G[s][d].time);
        for(i=t; i>=0; i--) {
            printf("%d",FRoad[i]);
            if(i)
                printf(" => ");
        }
        printf("
");
        printf("Distance = %d: ",G[s][d].length);
        for(i=k; i>=0; i--) {
            printf("%d",LRoad[i]);
            if(i)
                printf(" => ");
        }
    }
}