椭圆曲线算法的基本原理及实现

Posted 2020-11-14 gjqdream

1、基本概念

1）椭圆曲线方程的一般形式：y^2 = x^3 + a*x + b，其中要求满足不等式 4*a^3 + 27*b^2 ≠ 0

例如：y^2 = x^3 + x + 1 mod 23

2）椭圆曲线上的点的加法公式（适用于 P ≠ Q 的情况）：设 P = (x1, y1)，Q = (x2, y2)，P + Q = R = (x3, y3)，t = (y2-y1)/(x2-x1)，x3 = t^2 - x1 - x2，y3 = t*(x1 - x3) - y1

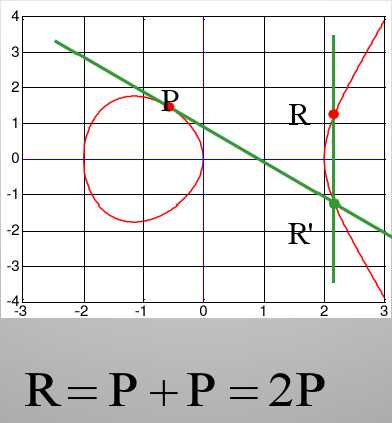
3）椭圆曲线上的点的加法公式（当上面的 P = Q 时）：P + P = R = (x3, y3)，t = (3*x1^2+a)/(2*y1)，x3 = t^2 - x1 - x1，y3 = t*(x1 - x3) - y1

 

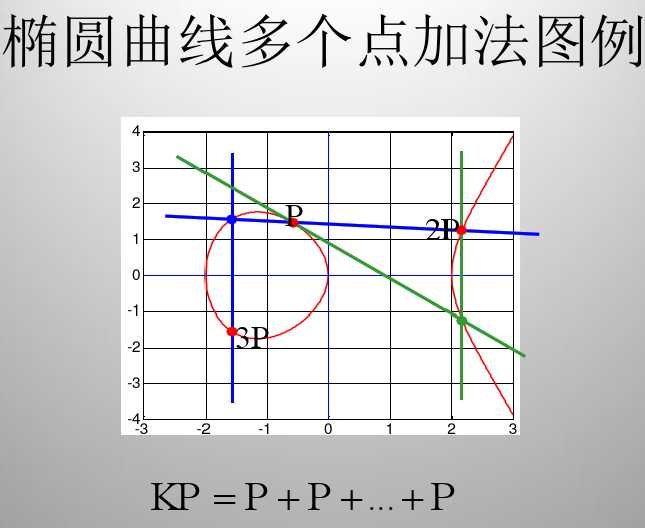
2、准备步骤

1）随机生成一个数 d 做私钥

2）选椭圆曲线上的一个点 P，计算 Q = d*P 做公钥

 

设 A 要加密 M 送给 B，B 的私钥为 d，公钥为 Q = d*P

3、加密过程

1）A 随机生成一个数 k

2）计算 k*P 和 k*Q

3）取 k*Q 的横坐标与 M 异或得到密文 C

4）A 发送 k*P 和密文 C 给 B

 

4、解密过程

1）B 用自己的私钥 d 计算 d*(k*P)

2）B 用 d*(k*P) 的横坐标与密文 C 异或得到 M

 

5、注解：

1）A 用 k*P 与 B 用 d*(k*P) = k*(d*P) = k*Q

2）经过两次异或得到原文（明文）

 

参考文档：

https://wenku.baidu.com/view/ff42b6610b1c59eef8c7b477.html

遇到的疑问：

1）Objct[] 数组不能直接转换为 ArrayList