动态规划-最长递增子序列

Posted 2021-03-03 dream-flying

1、问题：给出长度为N的数组，找出这个数组的最长递增子序列。 (递增子序列是指，子序列的元素是递增的） 

递推公式：

 

 

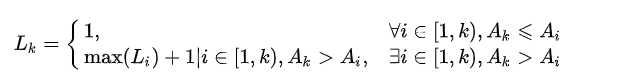
2、原理分析：假设开始计算位置i，当位置i之前的所有记录都 大于位置i的值时，L(i)  = 1； 当存在小于L(i)的位置时,比较所有情况，取最大值，L(i) = L(k)+1。

 

3、code：

 

　　（1）使用一维数据记录每个位置的最大上升子序列长度：keep[i] = L(i);

　　　

import java.util.Scanner;

/*
 * 求最长上升子串
 */
public class Main10_1 {
	public static void main(String args[] ) {
		Scanner s = new Scanner(System.in);
		int ar[] = {2,1,8,9,3,5,6};
		int len = ar.length;
		int keep[] = new int[len];
		int temp;
		int max = 1;
		keep[0] = 1;
		
		for(int i=1;i<len;i++) {
			int j;
			int count = 0;
			for(j=i-1;j>=0;j--) {
				//一点小变化，增加比较的次数
				//找到第一个小于ar[i]的值
				for(;(j>=0 && ar[j]>=ar[i]);j--);
				if(j>=0) {
					count = keep[j];
					temp = ar[j];
					for(j=j-1;j>=0;j--) {
						//等价于每个子序列只计算一次（末尾元素降序）
						if(ar[j]<ar[i] && ar[j]>temp) {
							temp = ar[j];
							count = Math.max(count,keep[j]);
						}
					}
				}
				/*
				最原始的方法，存在多余的计算
				if(ar[j]<ar[i]) {
					count = Math.max(count, keep[j]);
				}*/
			}
			keep[i] = count+1;
			max = max>keep[i]?max:keep[i];
		}
		for(int i=0;i<len;i++) {
			System.out.print(keep[i]+" ");
		}
		
		System.out.println("
"+max);
	}
}

　　（2）使用一位数组记录到达长度的最小元素：keep[i] = A(k){ 0<=k <= i} ,更小的值存在更大的概率与后续值构成升序序列。

　　　　》从而记录数组天然构成一个升序序列，可以使用二分查找。

package yrc2;

import java.util.Scanner;

public class Main10_2 {
	public static void main(String args[] ) {
		Scanner s = new Scanner(System.in);
		int ar[] = {2,1,8,9,3,5,6};
		int len = ar.length;
		int keep[] = new int[len+1];
		int keep_len = 1;
		keep[1] = ar[0];
		
		for(int i=1;i<len;i++) {
			int left = 1;
			int right =keep_len;
			while(left<=right) {
				int mid = (left+right)/2;
				if(keep[mid]<ar[i]) {
					left=mid+1;
				}else {
					/*
					 * 当keep[mid]==ar[i]也执行right = mid-1,
					 * 导致后续操作只会执行第一个if，最终left>right退出
					 * 并且left位置就是相等时mid的位置
					 */
					right = mid-1;
				}
				
			}
			keep[left] = ar[i];
			if(left>keep_len) {
				keep_len++;
			}
		}
		for(int i=1;i<=keep_len;i++) {
			System.out.print(keep[i]+" ");
		}
		System.out.println("
"+keep_len);
	}

}

博客参考：https://www.jianshu.com/p/b3580d3e4dab