B. Princesses and Princes

Posted 2021-03-03 love-chili

B. Princesses and Princes

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The King of Berland Polycarp LXXXIV has nn daughters. To establish his power to the neighbouring kingdoms he wants to marry his daughters to the princes of these kingdoms. As a lucky coincidence there are nn other kingdoms as well.

So Polycarp LXXXIV has enumerated his daughters from 11 to nn and the kingdoms from 11 to nn. For each daughter he has compiled a list of kingdoms princes of which she wanted to marry.

Polycarp LXXXIV is very busy, so he finds a couple for his daughters greedily one after another.

For the first daughter he takes the kingdom with the lowest number from her list and marries the daughter to their prince. For the second daughter he takes the kingdom with the lowest number from her list, prince of which hasn‘t been taken already. If there are no free princes in the list then the daughter marries nobody and Polycarp LXXXIV proceeds to the next daughter. The process ends after the nn-th daughter.

For example, let there be 44 daughters and kingdoms, the lists daughters have are [2,3][2,3], [1,2][1,2], [3,4][3,4], [3][3], respectively.

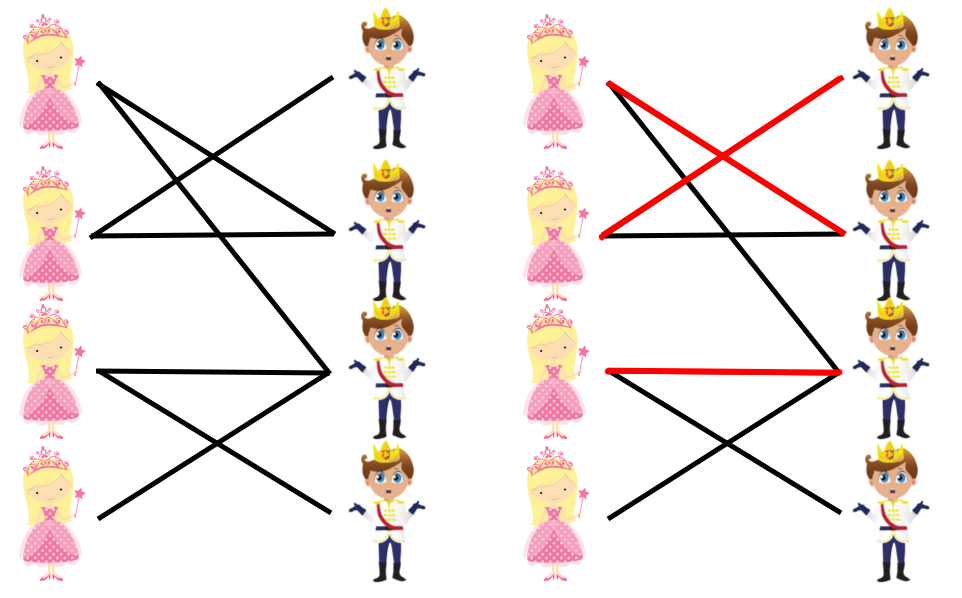
In that case daughter 11 marries the prince of kingdom 22, daughter 22 marries the prince of kingdom 11, daughter 33marries the prince of kingdom 33, leaving daughter 44 nobody to marry to.

Actually, before starting the marriage process Polycarp LXXXIV has the time to convince one of his daughters that some prince is also worth marrying to. Effectively, that means that he can add exactly one kingdom to exactly one of his daughter‘s list. Note that this kingdom should not be present in the daughter‘s list.

Polycarp LXXXIV wants to increase the number of married couples.

Unfortunately, what he doesn‘t have the time for is determining what entry to add. If there is no way to increase the total number of married couples then output that the marriages are already optimal. Otherwise, find such an entry that the total number of married couples increases if Polycarp LXXXIV adds it.

If there are multiple ways to add an entry so that the total number of married couples increases then print any of them.

For your and our convenience you are asked to answer tt independent test cases.

Input

The first line contains a single integer tt (1≤t≤1051≤t≤105) — the number of test cases.

Then tt test cases follow.

The first line of each test case contains a single integer nn (1≤n≤1051≤n≤105) — the number of daughters and the number of kingdoms.

Each of the next nn lines contains the description of each daughter‘s list. The first integer kk (0≤k≤n0≤k≤n) is the number of entries in the ii-th daughter‘s list. After that kk distinct integers follow gi[1],gi[2],…,gi[k]gi[1],gi[2],…,gi[k] (1≤gi[j]≤n1≤gi[j]≤n) — the indices of the kingdoms in the list in the increasing order (gi[1]<gi[2]<?<gi[k]gi[1]<gi[2]<?<gi[k]).

It‘s guaranteed that the total number of daughters over all test cases does not exceed 105105.

It‘s also guaranteed that the total number of kingdoms in lists over all test cases does not exceed 105105.

Output

For each test case print the answer to it.

Print "IMPROVE" in the first line if Polycarp LXXXIV can add some kingdom to some of his daughter‘s list so that the total number of married couples increases. The second line then should contain two integers — the index of the daughter and the index of the kingdom Polycarp LXXXIV should add to that daughter‘s list.

If there are multiple ways to add an entry so that the total number of married couples increases then print any of them.

Otherwise the only line should contain one word "OPTIMAL".

Example

input

Copy

5
4
2 2 3
2 1 2
2 3 4
1 3
2
0
0
3
3 1 2 3
3 1 2 3
3 1 2 3
1
1 1
4
1 1
1 2
1 3
1 4

output

Copy

IMPROVE
4 4
IMPROVE
1 1
OPTIMAL
OPTIMAL
OPTIM

Note

The first test case is depicted in the statement. Adding the fourth kingdom to the list of the fourth daughter makes her marry the prince of the fourth kingdom.

In the second test case any new entry will increase the number of marriages from 00 to 11.

In the third and the fourth test cases there is no way to add an entry.

In the fifth test case there is no way to change the marriages by adding any entry.

题意：

有n个公主和王子，每个公主都有0-n个喜欢的王子，匹配他们，如果全部匹配上输出OPTIMAL，否则输出IMPROVE，并输出一个未匹配的公主 和一个王子（你手动匹配的）。

思路：

题目给了一个前提条件：每位公主喜欢的王子都是从小到大给出的。所以我们创立一个set，并将里面装入1到n个数（可以看做是王子），再开始遍历每个公主，一旦一个公主匹配上就结束，只到最后。如果一个公主没有匹配上就记录这个数（公主）。

再从set里面取出一个数（王子）就可以了。

代码：

#include<iostream>
#include<bits/stdc++.h>

using namespace std;

int main()
{
    int t;
    cin>>t;
    while(t--)
    {

        int n;
        cin>>n;
        set<int > st;
        for(int i=1; i<=n; i++)
            st.insert(i);
        int index,value,flag=0;
        for(int i=0; i<n; i++)
        {
            int m;
            cin>>m;
            int f=0;
         //   set<int>::iterator it;
            for(int j=0; j<m; j++)
            {
                int x;
                cin>>x;
                if(st.find(x)!=st.end()&&f==0)
                {

                    st.erase(x);
                    f++;
                }

            }
           /* for(it = st.begin(); it!= st.end(); it++)
                    cout << *it << " ";
                puts("");*/
            if(f==0)
            {
                index=i+1;
                flag++;
            }
        }
        if(flag!=0)
        {
            cout<<"IMPROVE"<<endl;
            cout<<index<<" "<<*(st.begin())<<endl;
        }
        else
            cout<<"OPTIMAL"<<endl;
    }

    return 0;
}

View Code