并查集之图的同构(同构图)-概念未清

Posted 2021-03-03 waryan

同构图：图论当中的术语，假设G=(V,E)和G1=(V1，E1)是两个图，如果存在一个双射m：V→V1，使得对所有的x,y∈V均有xy∈E等价于m(x)m(y)∈E1，则称G和G1是同构的,这样的一个映射m称之为一个同构，如果G=G1，则称他为一个自同构

 

 

HDU3926-Hand in Hand

 

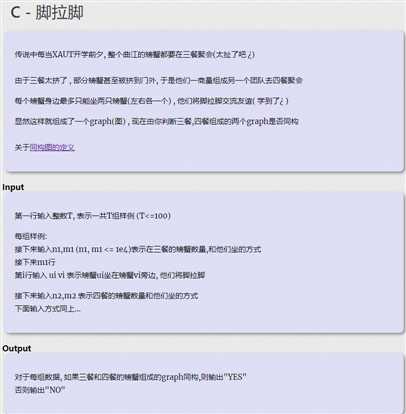
解题思路：判断两个图形成的链的数量和环的数量是否相等即可(链上的点数目也要相等)

#include <iostream>
#include<algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include<map>
#include<set>
#include<sstream>
#define INF 0x3f3f3f3f
#define DOF 0x7f7f7f7f
#define mem(a,b) memset(a,b,sizeof(a))
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
typedef long long ll;
using namespace std;
const int maxn=10010;
int f[maxn],ran[maxn],n1,m1,n2,m2,pos1,pos2,iscircle[maxn];
struct node
{
    int num,iscircle;
}arr1[maxn],arr2[maxn];
bool cmp(node a,node b)
{
    if(a.num!=b.num) return a.num<b.num;
    else return a.iscircle>b.iscircle;
}
void init(int n)
{
    mem(iscircle,0);
    for(int i=1;i<=n;++i)
        f[i]=i,ran[i]=1;
}
int Find(int x){
    return x==f[x]?f[x]:f[x]=Find(f[x]);
}
void Union(int x,int y)
{
    x=Find(x),y=Find(y);
    if(x==y){
        iscircle[x]=1;return ;
    }
    ran[y]+=ran[x];
    f[x]=y;
}
bool judge()
{
    if(pos1!=pos2) return false;
    sort(arr1,arr1+pos1,cmp);
    sort(arr2,arr2+pos2,cmp);
    for(int i=0;i<pos1;++i){
        if(arr1[i].num!=arr2[i].num) return false;
        if(arr1[i].iscircle!=arr2[i].iscircle) return false;
    }
    return true;
}
int main()
{
    int T;int cas=1;
    scanf("%d",&T);
    while(T--){
        int u,v;
        scanf("%d%d",&n1,&m1);
        init(n1);
        for(int i=0;i<m1;++i){
            scanf("%d%d",&u,&v);
            Union(u,v);
        }
        pos1=0,pos2=0;
        for(int i=1;i<=n1;++i){
            if(i==Find(i)){
                arr1[pos1].num=ran[i];
                arr1[pos1++].iscircle=iscircle[i];
            }
        }
        scanf("%d%d",&n2,&m2);
        init(n2);
        for(int i=0;i<m2;++i){
            scanf("%d%d",&u,&v);
            Union(u,v);
        }
        if(n1!=n2||m1!=m2){
            printf("Case #%d: NO
",cas++);
            continue;
        }
        for(int i=1;i<=n2;++i){
            if(i==Find(i)){
                arr2[pos2].num=ran[i];
                arr2[pos2++].iscircle=iscircle[i];
            }
        }
        if(judge()) printf("Case #%d: YES
",cas++);
        else printf("Case #%d: NO
",cas++);
    }
    return 0;
}