二叉搜索树的建立查找删除等相关操作实现及对于删除操作的详细解释

Posted 2021-03-03 yuyuan-bb

前记，最近开始了保研准备，故记录一下复习过程。
这次就对二叉树做一下实现。

在以下操作中，稍复杂的应该是删除，本想采用递归的方式构造删除函数，奈何最后还是按照自己的想法写了，本博客将对我的实现稍作描述，如有错误请指正，实现的方法中肯定也有很多累赘之处，也请多多指出。

首先将所有的情况分为三种：

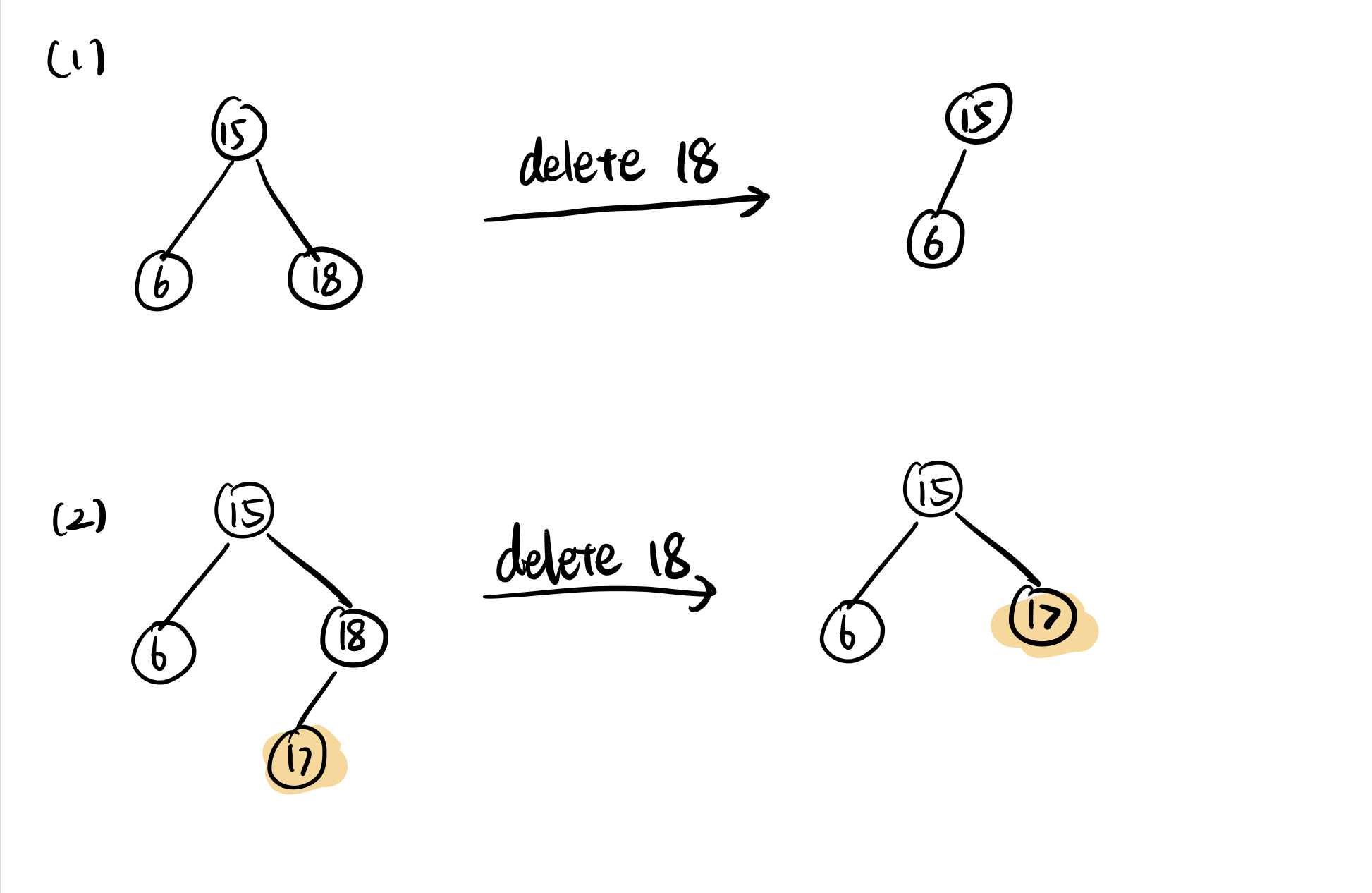
• 被删除的节点没有儿子节点，对应（1）。
• 被删除的节点有一个儿子节点，此时只需要将儿子节点上移至原有的节点处，对应（2）。
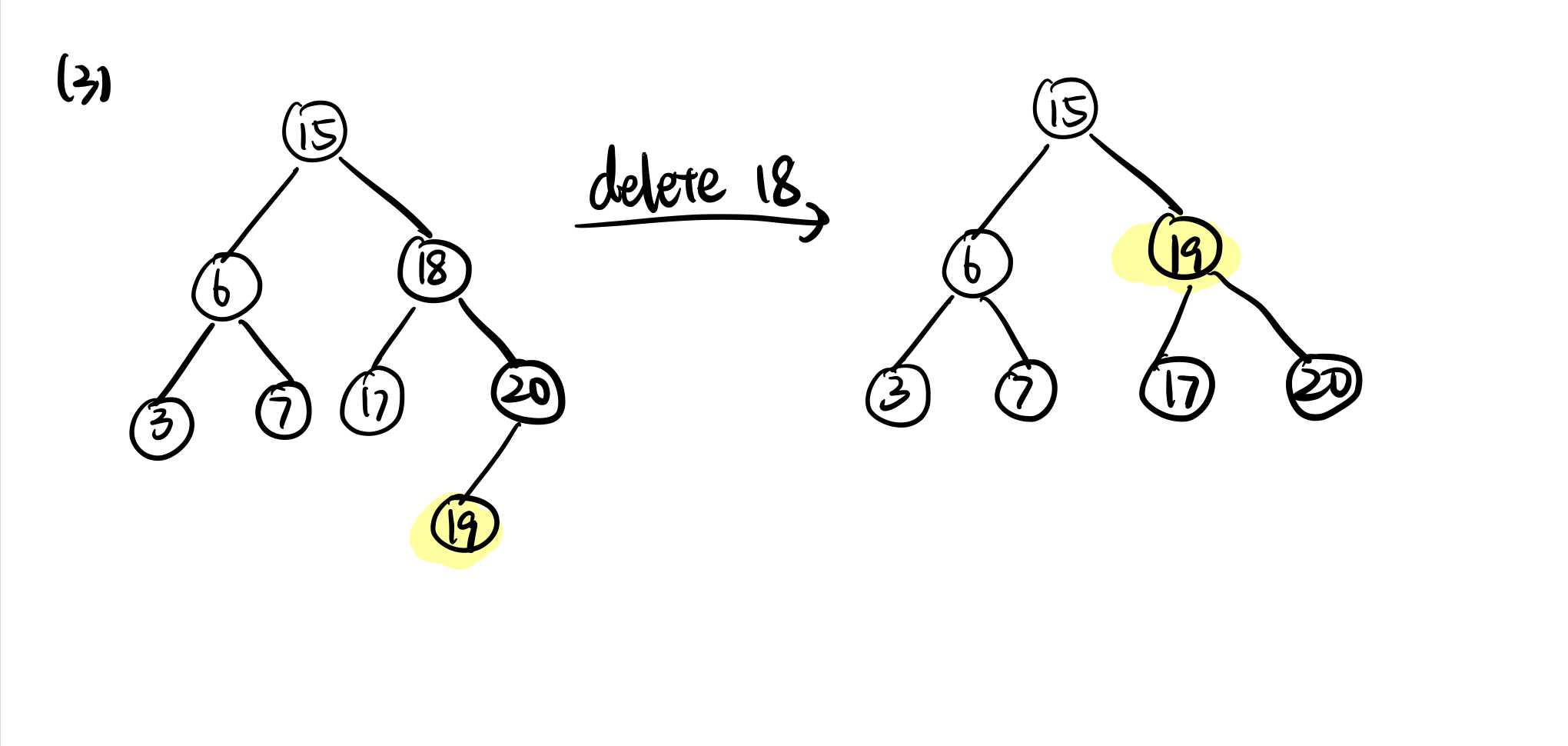
• 被删除的节点有两个儿子节点，此时可以选择左子树的最大值或者右子树的最小值对应的节点代替原有被删除的节点，对应（3）。

其中，第一种情况可以视为特殊的第二种情况，可以合并为第二种情况。实现时只需要记住被删除节点的父节点(parentNode)以及被删除节点相对于父节点的位置即可，在这里用flag表示，flag为0代表被删除节点是父节点的左儿子。

而第三种情况下，我选择的是寻找被删除节点右子树的最小值，并将情况分为了以下两种情况：

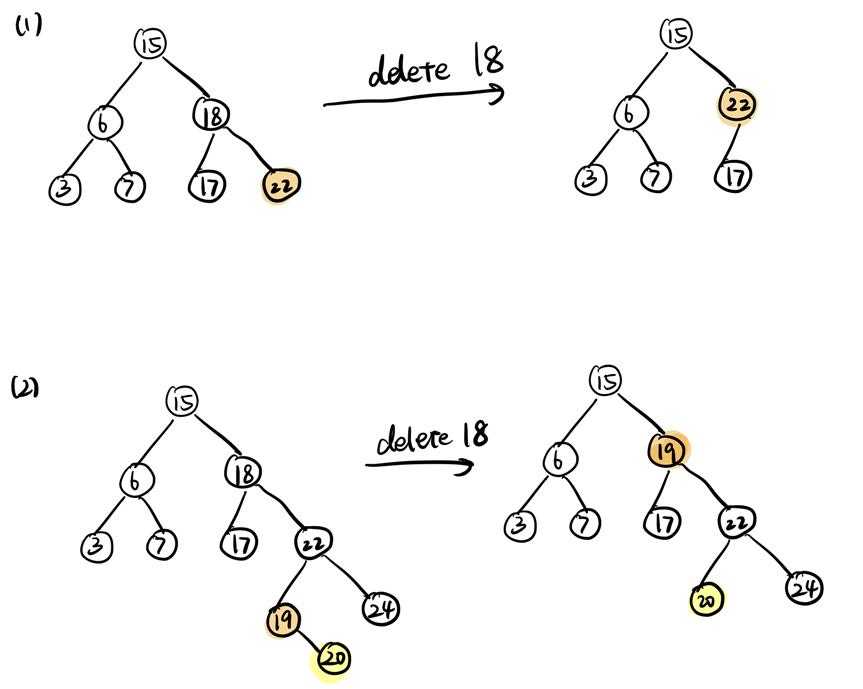
• 情况（1）的特点是，被删除节点的右子树仅为一个节点，在这种情况下只需要将被删除节点对应的data修改为右子树的data（22）即可。
• 情况（2）即除（1）外其他情况

下面对情况（2）进行分析：

pTemp指向被删除节点（但在下面的程序中是pTemp2）
p指向经过寻找以后最终找到的右子树最小值对应节点
parentNode指向最小值对应节点的父节点

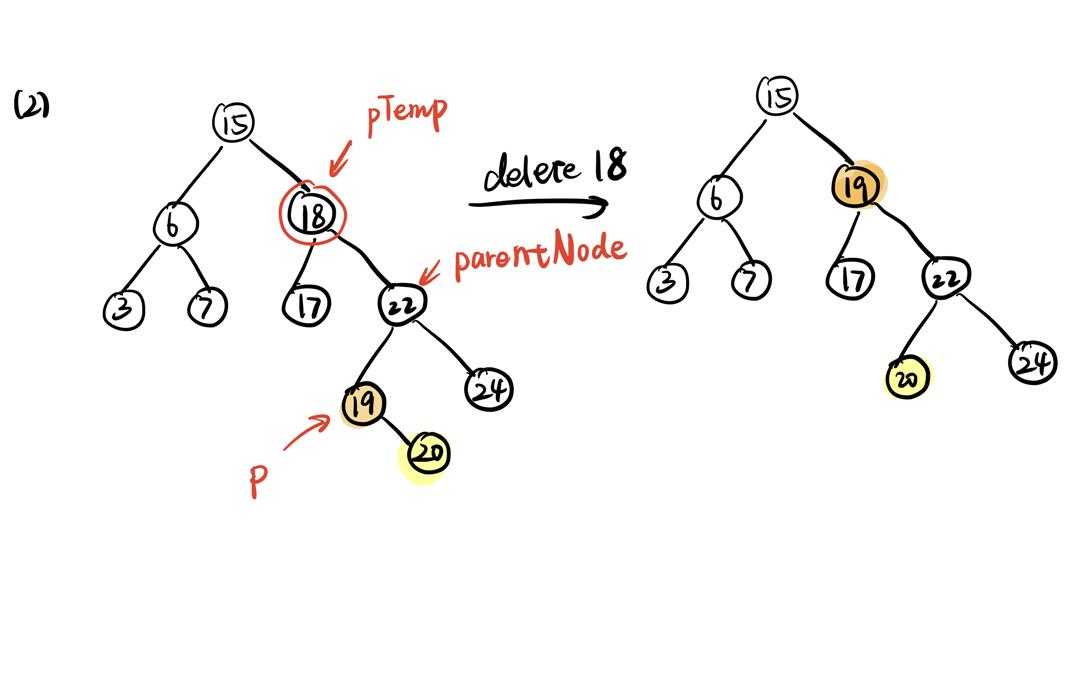
首先，我们用最小值节点代替被删除节点的位置，那么这意味着这个最小值节点的子树会受到影响，我们需要找到他们未来应该接到哪里。

被删除节点的代替可以直接用赋值实现

pTemp->data = p->data;

因为最小值节点（上图节点19）一定是这棵树的最左的儿子，因此它没有左儿子，只可能有右儿子。我们只需要考虑这个节点的右子树应该放在哪里，经过观察与大小比较，我们可以发现这个最小值节点的右子树未来应该接在这个节点的父节点（parentNode,上图22）的左儿子处。
于是有

parentNode->left = p->right;

最后只要释放掉最小值对应节点即可。

free(p)

详细的代码如下：

#include<iostream>
#include<stdlib.h>

#include <cstdlib>
#include <stdio.h>

typedef struct TreeNode {
   struct TreeNode* left;
   struct TreeNode* right;
   int data;

}TreeNode, * TreeP;
using namespace std;
TreeP findMin(TreeP root);
TreeP insertNode(TreeP root, int val) {
   TreeP pTemp = NULL;

   if (!root) {
   	root = (TreeNode*)malloc(sizeof(TreeNode));
   	//root = new TreeNode();
   	root->data = val;
   	root->left = NULL;
   	root->right = NULL;
   	return root;
   }
   else {
   	TreeP p = root;
   	while (p) {
   		pTemp = p;
   		if (val < p->data) {
   			p = p->left;
   		}
   		else if (val > p->data) {
   			p = p->right;
   		}

   	}
   	TreeP tNode = (TreeNode*)malloc(sizeof(TreeNode));
   	tNode->data = val;
   	tNode->left = NULL;
   	tNode->right = NULL;
   	if (pTemp->data > val) {
   		pTemp->left = tNode;
   	}
   	else {
   		pTemp->right = tNode;
   	}
   
   	return root;

   }
   
}

//删除，共有三种情况
bool deleteNode(TreeP root, int val) {
   TreeP p = root, parentNode = root,pTemp2 = NULL;
   int flag = -1;
   //找到要删除的节点
   if (!p) {
   	return false;
   }
   
   while (p) {
   	;
   	if (p->data == val) {
   		break;
   	}
   	else if (p->data > val) {
   		parentNode = p;
   		p = p->left;
   		flag = 0;
   	}
   	else if (p->data < val) {
   		parentNode = p;
   		p = p->right;
   		flag = 1;
   	}

   }
   if ( !p->right) {
   	
   	if (!flag) {
   		parentNode->left = p->left;
   			
   	}
   	else {
   		parentNode->right = p->left;
   		//p = p->left;
   	}
   	free(p);
   }
   else if (!p->left) {
   	if (!flag) {
   		parentNode->left = p->right;
   	}
   	else {
   		parentNode->right = p->right;
   	}
   	free(p);
   }
   //如果有两个节点
   else {
   	pTemp2 = p;
   	parentNode = p;
   	//找到右子树上最小的值
   	p = p->right;
   	

   	while (p->left) {
   		parentNode = p;
   		p = p->left;
   	}
   	
   	pTemp2->data = p->data;

   	if (pTemp2 == parentNode) {
   		parentNode->right = NULL;
   	}
   	else {
   		parentNode->left = p->right;
   	}

   	
   	free(p);
   }
   	
   return true;

}

TreeP findMin(TreeP root) {

   if (root) {
   	if (root->left == NULL) {
   		return root;
   	}
   	findMin(root->left);
   }
   else {
   	return root;
   }

}

TreeP findMax(TreeP root) {

   if (root) {
   	if (root->right == NULL) {
   		return root;
   	}
   	findMin(root->right);
   }
   else {
   	return root;
   }

}

TreeP findParentNode(TreeP root, TreeP node) {
   if (root) {
   	if (root->left == node || root->right == node) {
   		return root;
   	}
   	findParentNode(root->left,node);
   	findParentNode(root->right,node);
   }
   else {
   	return root;
   }

}


TreeP findNode(TreeP root, int val) {
   TreeP p = root;
   if (p) {
   	if (p->data == val) {
   		return p;
   	}
   	findNode(p->left, val);
   	findNode(p->right, val);
   }
}

void travelPreOrder(TreeP p) {
   if (p) {
   	cout << p->data << " ";
   	travelPreOrder(p->left);
   	travelPreOrder(p->right);
   }
   
}

int main() {

   TreeP p = NULL;
   int val = 0;
   int num;
   cin >> num;
   while (num > 0) {
   	cin >> val;
   	p = insertNode(p, val);
   	num--;
   }

   travelPreOrder(p);
   cout << endl;
   p = findNode(p, 18);
   cout << p->data<< endl;
   

}