Codeforces Round #629 (Div. 3) F - Make k Equal （离散化 树状数组维护前缀和）

Posted 2021-03-03 aaronchang

https://codeforces.com/contest/1328/problem/F

 

首先把a数组处理成pair对（num,cnt），表示数字num有cnt个，然后按num升序排序离散化一下。

对于一个数x，若想使得小于x的数字都变成x，必须先把所有小于x的数变成x-1，然后再+1变成x。

同理，要使得大于x的数变成x，必须把所有大于x的数字变成x+1，然后再-1变成x。

以上是题意所要求的必须操作。

思路：

1. 用f[i]数组记录离散化后前i大的数字的总数，那么对于任意第i大数字，可以靠f[i]数组轻易求出大于num[i]的数字个数和小于num[i]的数字个数

2. 用一个树状数组维护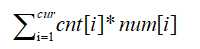  cur代表离散化后一共cur个不同的数字。

 

 

3.对于任意第i大数字，若k<=cnt[i]，则ans = 0，不用做任何操作，这是很显然的结论

4.对于任意第i大数字，若k>cnt[i]，设 d = k - cnt[i]，分为以下三种情况讨论：

    (i) 比第i个数字大的数字有大于d个时，可以把大于num[i]的数字移动到num[i]+1的位置，这个过程的花费设为sum，再把d个数字移动到num[i]，花费sum+d，则即可满足条件

    (ii)比第i个数字小的数字有大于d个时，可以把小于num[i]的数字移动到num[i]-1的位置， 这个过程的花费设为sum，再把d个数字移动到num[i]，花费sum+d，则即可满足条件

    (iii)比第i个数字大的数字小于d个和比第i个数字小的数字小于d个同时发生，那么需要把大于num[i]和小于num[i]的数字全部分别移动到num[i]+1和num[i]-1，这整个过程花费记为sum3，再把d个数字移动到num[i]，总花费sum3+d，满足条件。

针对每个num[i]做以上三种操作，取min即可

 

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 const int maxn = 2e5+5;
 5 ll c[maxn],a[maxn],f[maxn];
 6 int n,k;
 7 struct node{
 8     ll cnt,num;
 9     bool operator < (const node &b){
10         return num<b.num ;
11     }
12 }p[maxn],t[maxn];
13 ll lowbit(ll x){
14     return x& -x;
15 }
16 void add(ll x,ll k){
17     while(x<=n){
18         c[x] = c[x] + k;
19         x = x + lowbit(x);
20     }
21 }
22 ll getsum(ll x){
23     ll ans = 0;
24     while(x>=1){
25         ans +=c[x];
26         x = x-lowbit(x);
27     }
28     return ans;
29 }
30 int main(){
31     scanf("%d%d",&n,&k);
32     for(int i = 1;i<=n;i++) {
33        scanf("%lld",&p[i].num );    
34     }
35     sort(p + 1,p + 1 +n);//离散化
36     t[1].num = p[1].num,t[1].cnt = 1,f[1] = 1; 
37     int cur = 1;
38     for(int i = 2;i<=n;i++){
39         if(p[i].num !=t[cur].num ) t[cur+1].num = p[i].num ,t[cur+1].cnt = 1,cur++,f[cur]=f[cur-1]+1;
40         else t[cur].cnt ++,f[cur]++;//处理f函数和t数组
41     }
42     for(int i = 1;i<=cur;i++){
43         add(i,t[i].cnt *t[i].num );//维护前缀和
44     }
45     ll ans = 1e15+5;
46     for(int i = 1;i<=cur;i++){
47         if(k<=t[i].cnt ) {ans = 0;break;} //存在k>=cnt[i]直接break，ans = 0
48         else{
49             ll d = k - t[i].cnt ;//剩余需要d个移动到num[i]
50             if(f[cur]-f[i]>=d){
51                 ll sum = getsum(cur) - getsum(i) - (f[cur]-f[i]) *(t[i].num+1);
52                 ans = min(ans,sum+d);
53                 
54             }
55             if(f[i-1]>=d){
56                 ll sum = f[i-1]*(t[i].num -1)- getsum(i-1);
57                 ans = min(ans,sum+d);
58             }
59             if(f[cur]-f[i]<d && f[i-1]<d){
60                 ll sum = getsum(cur) - getsum(i) - (f[cur]-f[i]) *(t[i].num+1);
61                 sum = sum + f[i-1]*(t[i].num-1) - getsum(i-1);
62                 ans = min(ans,sum+d);            
63             }
64         }
65     }
66     cout<<ans;
67     return 0;
68 }