杂题选讲1

Posted 2021-03-02 athosd

把序列排序后
问题转化为子序列两两之间的异或和大于等于k
用户(Trie)树优化(dp)
因为不满足单调性所以不能用二分来优化

(ans=sum_{i=1}^{n}n%i)
(ans=sum_{i=1}^{n}(n-n/i*i))
(ans=n^2-sum_{i=1}^{n}i*(n/i))
从实际含义入手
(ans=n^2-sum_{i=1}^{n}d1(i))
((dk(i)=sum_{j|i}j^k))
线性预处理即可
复杂度(O(N+T))

原先做(SA)的题时用过这个套路
枚举长度(len*2),每隔(len)插一个点
这样对于相邻两个关键点求出最长公共前缀和最长公共后缀
那么答案串便可以在这个区间里滚动
类似哈希的去求贡献
假如(S[i+1]=0)，根据平方串的性质可以让(H[i]=0)来解决前导零

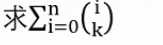
其中ki给定
考虑对于每个组再分组
每个组被(k_i)个人分成了(k_i+1)个小组
发现有(k_i)个小组大于(0，1)个小组可能等于(0)
为了统一化，让前(k_i)个小组不包含被选中的人，
条件都变成每个小组非负
直接组合数计算即可

转化为其他组在(1)之前被丢掉的概率之和
(i)的贡献便是(frac{A[i]}{A[i]+A[1]})

是原来一道提答题的部分分
对于每个数(x)它自主删的概率便是(frac{1}{d(x)})
加和便是答案
这道题需要用到(min_25)筛

神奇的期望线性性！！
设(E_G)代表每拿一个蓝球绿球被拿的期望个数
(E_G=(E_G+1)*frac{G}{B+G})
(E_G=frac{G}{B})
所以绿球的贡献便是(frac{GK}{B})
对于每个红球可以分开考虑
它不被拿出的概率(P_R=(frac{1}{B+1})^k)
红球的贡献便是(E_R=R*(1-P_R))

考虑预处理出可能对答案造成贡献的点对
对于一个右端点(r)，左端点(x,y)
一定满足，(a_x<a_y)
并且满足(a_r-a_y<a_y-a_x)
即(2*(a_r-a_y)<a_r-a_x)
也就是说差值至少变为了一半
所以对于一个确定的右段点，最多有(log)个
拿数据结构去求出并且维护即可