积蓄程度

Posted 2021-03-02 jjl0229

287. 积蓄程度

有一个树形的水系，由 N-1 条河道和 N 个交叉点组成。
我们可以把交叉点看作树中的节点，编号为 1~N，河道则看作树中的无向边。
每条河道都有一个容量，连接 x 与 y 的河道的容量记为 c(x,y)。
河道中单位时间流过的水量不能超过河道的容量。
有一个节点是整个水系的发源地，可以源源不断地流出水，我们称之为源点。
除了源点之外，树中所有度数为 1 的节点都是入海口，可以吸收无限多的水，我们称之为汇点。
也就是说，水系中的水从源点出发，沿着每条河道，最终流向各个汇点。
在整个水系稳定时，每条河道中的水都以单位时间固定的水量流向固定的方向。
除源点和汇点之外，其余各点不贮存水，也就是流入该点的河道水量之和等于从该点流出的河道水量之和。
整个水系的流量就定义为源点单位时间发出的水量。
在流量不超过河道容量的前提下，求哪个点作为源点时，整个水系的流量最大，输出这个最大值。
输入格式
输入第一行包含整数T，表示共有T组测试数据。
每组测试数据，第一行包含整数N。
接下来N-1行，每行包含三个整数x,y,z，表示x，y之间存在河道，且河道容量为z。
节点编号从1开始。
输出格式
每组数据输出一个结果，每个结果占一行。
数据保证结果不超过2^31?1。
数据范围
N≤2?10^5
输入样例：
1
5
1 2 11
1 4 13
3 4 5
4 5 10
输出样例：
26

暴力的方法是枚举根节点，复杂度是O(n^2)，我们需要优化成一个线性或者log的复杂度
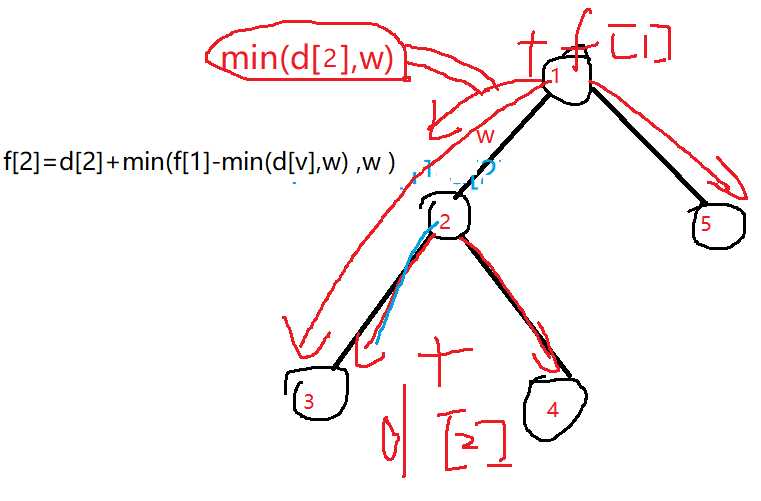
首先我们任取一个非叶子节点作为根节点root，统计所有节点的d，d[u]表示root作为根节点u向它子树可以向所有子节点流的最大水量，f[u]表示它作为根节点的最大水量，那么d[root]就是把root作为根节点的最大水量。对于root的子节点u，如果把u作为根节点，那么他的最大水量为它向下流的水量加上它向上流的水量，向下流的就是d[v]，向上流的水量是min(w:u与root边的容量，f[u]-min(d[v],w)：父节点u作为为整棵树根的节点时的最大水量减去向子节点v流的水量即u向其他节点流的最大水量) ，(注意叶子节点的d无穷大，统计f时不算它的d)，这样得到的就是以u为整棵树根节点的最大水量

#include<bits/stdc++.h>
using namespace std;
const int N=200010,INF=0x3f3f3f3f;
int h[N],d[N],f[N],idx,ind[N],root;
struct eg{
	int v,w,nex;
}e[N*2];
void add(int u,int v,int w){
	e[idx]=(eg){v,w,h[u]};
	h[u]=idx++;
}
void dfs_d(int u,int pre){
	if(ind[u]==1) {
		d[u]=INF;
		return ;
	}
	d[u]=0;
	for(int i=h[u];~i;i=e[i].nex){
		int v=e[i].v,w=e[i].w;
		if(v==pre) continue;
		dfs_d(v,u);
		d[u]+=min(d[v],w);
	}
}
void dfs_f(int u,int pre){
	for(int i=h[u];~i;i=e[i].nex){
		int v=e[i].v,w=e[i].w;
		if(v==pre) continue;
		if(ind[v]==1){
			f[v]=min(f[u]-min(w,d[v]),w);
		}
		else {
			f[v]=d[v]+min(f[u]-min(w,d[v]),w);
			dfs_f(v,u);
		}
	}
}
int main(){
	int T;
	scanf("%d",&T);
	while(T--){
		int n;
		scanf("%d",&n);
		memset(h,-1,sizeof h);idx=0;
		memset(ind,0,sizeof ind);
		for(int i=1;i<n;++i){
			int u,v,w;
			scanf("%d%d%d",&u,&v,&w);
			add(u,v,w);add(v,u,w);
			ind[u]++;ind[v]++;
		}
		root=1;
		while(root<=n){
		    if(ind[root]>1) break;
		    ++root;
		} 
		if(root>n) {
		    cout<<e[1].w<<endl;
		    continue;
		}
		dfs_d(root,-1);
		f[root]=d[root];
		dfs_f(root,-1);
		int res=0;
		for(int i=1;i<=n;++i) res=max(res,f[i]);
		cout<<res<<endl;
	}
	return 0;
}