线性代数的本质行列式逆矩阵列空间秩零空间

Posted 2021-03-02 veeupup

线性代数的本质，源视频 https://www.bilibili.com/video/BV1ys411472E

目录

• 行列式
• 逆矩阵
• 秩
• 列空间与零空间
• 非方阵

行列式

我们已经知道了矩阵的线性变换的意义，我们这节来学习行列式。

我们现在想象一些线性变换，有一些将空间向外拉伸，有些将空间向内挤压。

我们需要测量一个区域被拉伸或者被挤压的程度将会很有用，更具体一点，也就是测量一个给定的区域面积增大或者减小的比例。

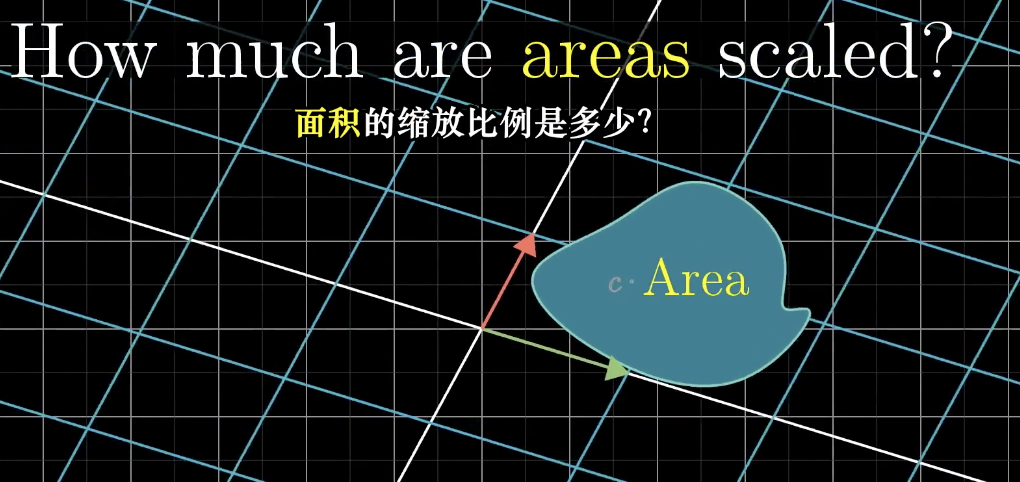
比如下面这样的线性变换矩阵，将原来面积为 1 的区域变成了长度为 3 宽度为 2 的矩阵，所有原来区域的面积都变味了最初的 6 倍。

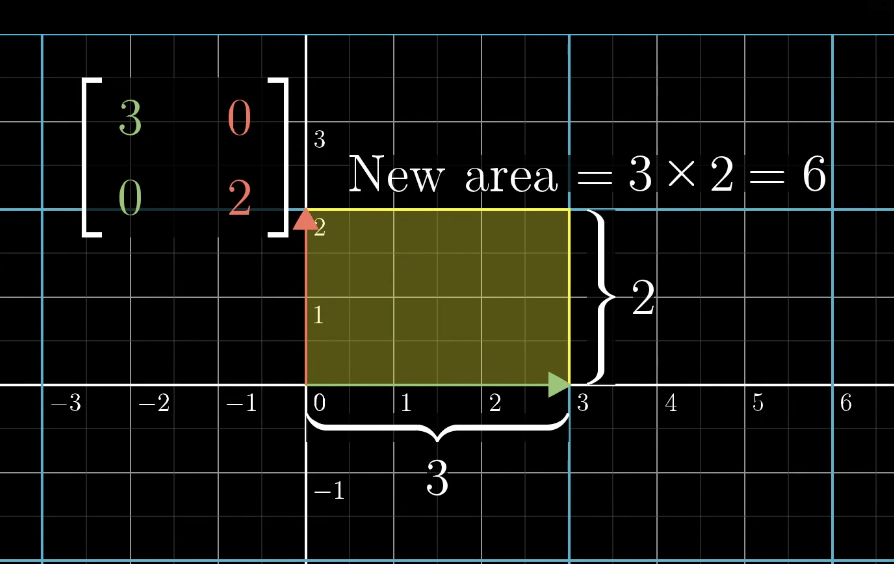
而下面这个线性变换之后，基向量对应的小方格的面积仍然不变，所以变换后的面积不变。

事实上，我们只需要计算出下面一个基本方格变化的大小，就可以推算出所有方格的面积变化，这是因为所有的网格都是平行等距分布的。

也就是说

这个特殊的缩放比例，即线性变换改变面积的比例，被称为这个变换的行列式

如果某个图形不是矩阵，我们只需要使用微元法分解为无数个小矩形即可。

特殊的，当一个行列式的值为 0 的时候，这个变换就将空间压缩到了更小的维度上。

当行列式的值为负的时候，代表什么意义呢？

如果是在二维空间想象成一张纸，一个线性变换的值为负，就好像把纸翻到了另一面。我们成这样的变换为改变了空间的定向的改变。但是此时行列式的值的绝对值仍然是线性变换改变空间面积的比例。

为什么这个值会是负数呢？

当i 和 j 逐渐靠近的时候，他们之间的面积会逐渐减小为0，而当i跑到j的右边的时候，这个值变成负数就很自然了。

这就是在二维空间中对线性变换行列式值意义的解释。

那么在三维空间中，我们看到的就是一个小立方体，当变换后，立方体就可以变成一个平行六面体，行列式给出的是平行六面体的体积。

在三维空间中行列式的值为负数，代表空间定向变了，而我们通常用右手坐标系和左手坐标系来代表这种变换。

这样应该就很好理解了。

而对于行列式值的计算也就理所当然，计算出改变的面积即可。

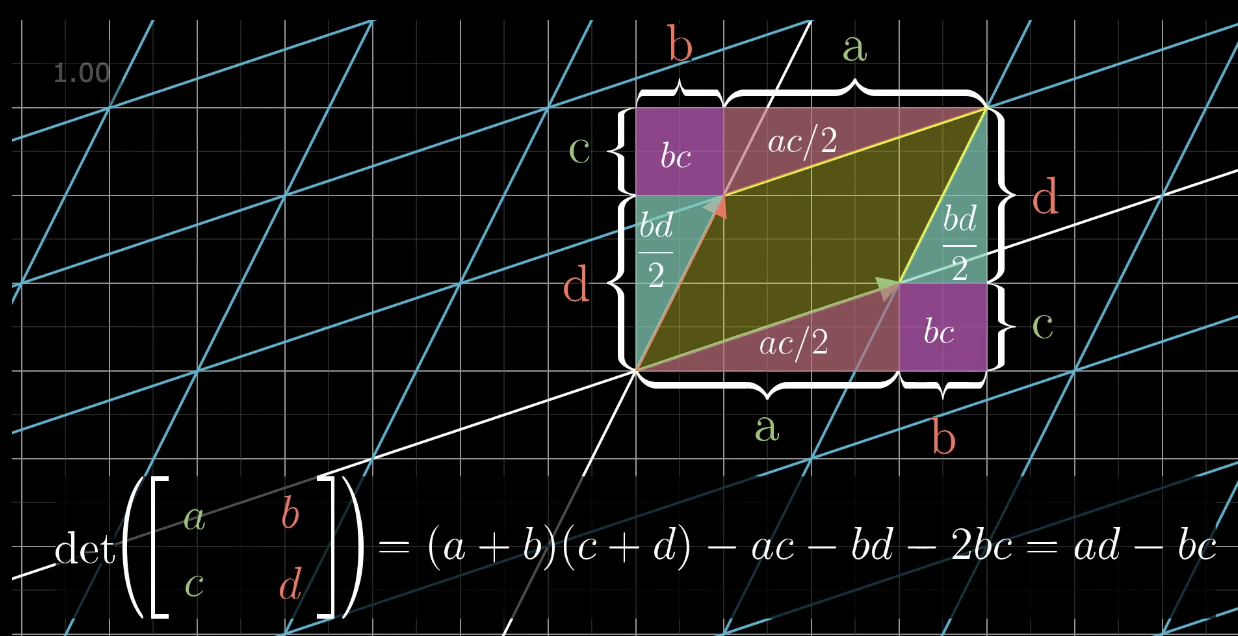
逆矩阵

我们要通过线性变换的方式来看待逆矩阵，矩阵的秩，列空间与零空间。

矩阵能够代表一系列含有未知数的方程，但是需要满足以下条件：

• 在每一个方程中，所有的未知量都只有常系数，而且这些未知量之间只进行加和。

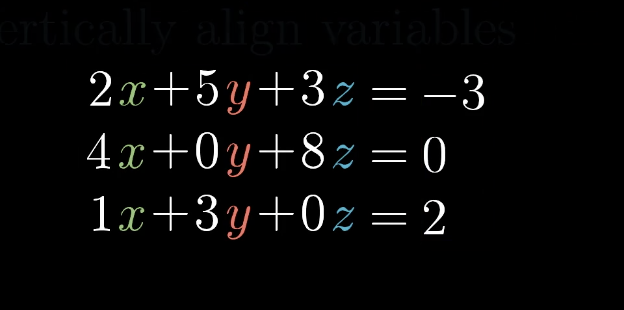
我们将每个未知数对齐，补充好为 0 的系数，此时我们就得到了线性方程组。

我们可以吧所有的方程合并成一个矩阵，分为以下三部分：

1. 常系数矩阵
2. 未知数向量
3. 常数向量

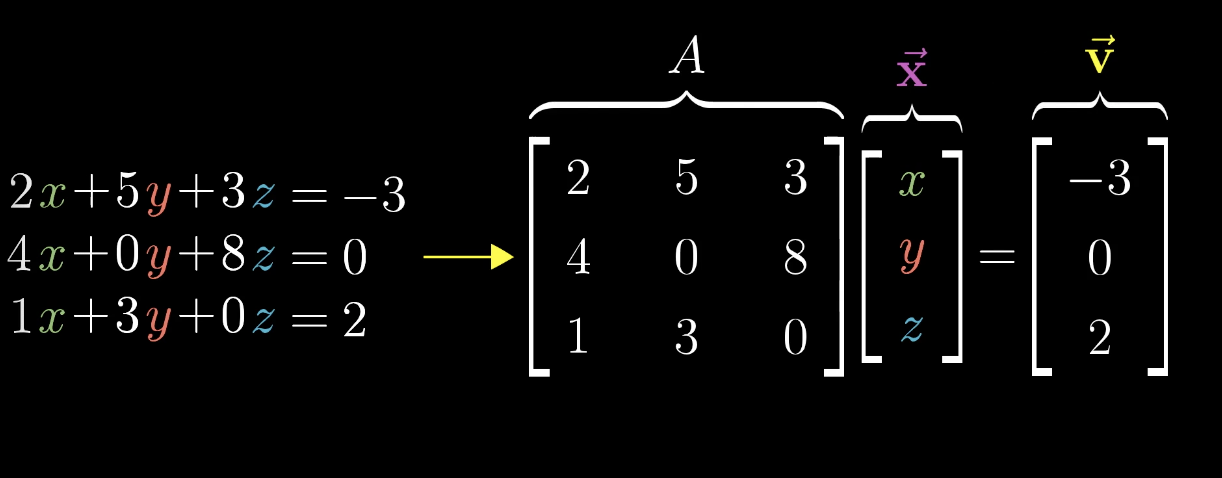
这不仅是一种较好的书写方式，也具有他的几何意义：

A 代表一种线性变换，我们需要找到一个向量 x 经过 A 的变换后与向量 v 重合。

我们考虑两种情况：

1. A 行列式的值不为 0

此时我们已经知道了一个线性变换 A 以及变换后的 v 向量，我们需要将 v 向量还原到变换之前的状态，也就是 x 向量，我们需要做出一个相反的线性变换将这个向量变为之前的状态即可。

我们称这个线性变换为之前线性变换 A 的逆矩阵。

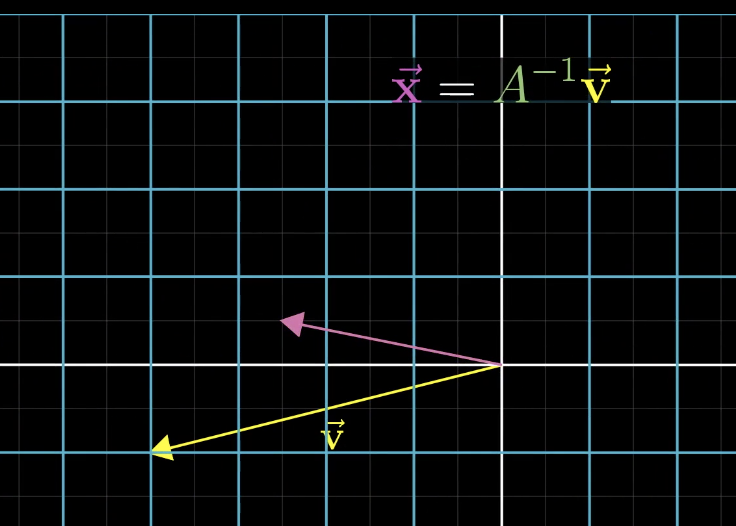
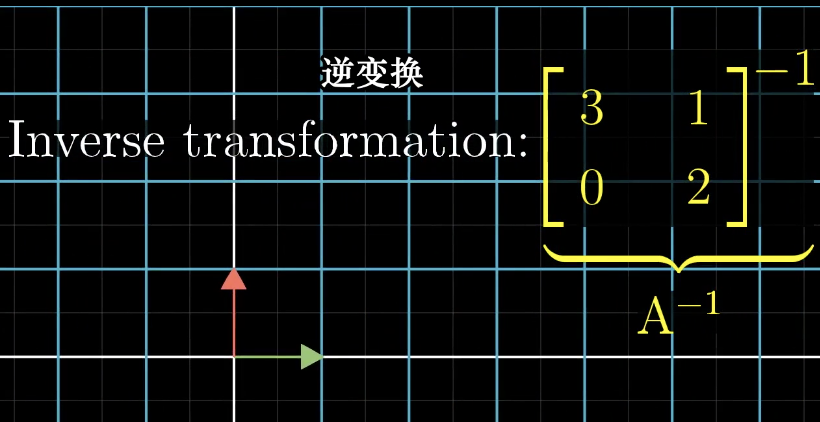
例如，我们先进行一个顺时针旋转90度的线性变换，然后再进行一个逆时针旋转90度的线性变换就可以回到之前的状态。

当我们找到了 A 的逆矩阵，我们就可以两边同时乘以 A 的逆矩阵，就可以得到 x 的解。

那么我们对于当方程数目和未知数相同的一个方程组，我们基本就可以确定它存在唯一解（或者没有解），你可以想象到旋转之后旋转回去的方式即可。

其实对于一个高阶的方程组，只要这个变换A不将空间压缩到一个更低的维度上，也就是行列式的值不为0，那么它就存在逆矩阵将其变回原来的向量。。

2. 当A的行列式的值为0的时候

此时在而二维空间线性变换就是一条直线，我们当然不可能吧一条线“解压缩”成一个平面。对于更高阶的线性变换也是如此。

但是当一个 A 的行列式的值为 0 的时候，也有可能存在解，这是因为如果一个变换将平面变成一条直线，而这个向量 v 刚好也在这条直线上，则此时就存在无数个解（都在这条直线上）。

秩

当一个变换的结果为一条直线的时候，我们称这个变换的秩为 1，也就是一维的。

当一个变换的结果为一个平面的时候，我们称这个变换的秩为 2，也就是二维的。

……

由此我们得到秩代表的意义，秩代表着变换后空间的维数。

对于 2x2 的矩阵，秩的最大值为 2。但是对于一个 3x3 的矩阵，当秩为 2 的时候就代表这个矩阵被压缩成一个平面了。

列空间与零空间

不论是一条直线，一个平面还是三维空间等，所有可能的变换的结果的集合被称为矩阵的 列空间。

我们知道矩阵的列代表矩阵的基向量变换后到达的位置，变换后的基向量张成的空间就是列空间，换句话说，列空间就是矩阵的列所张成的空间。

更精确的秩的定义式列空间的维数，当秩达到最大时，代表列数和秩相等，称之为满秩（full rank）。

注意，零向量一定会被包含到向量空间中，因为零向量的位置一直不变。
对于一个满秩变换来说，唯一能在变换后落在原点的就是零向量自身。但是对于非满秩的矩阵来说，会有一系列的向量在变换后落在原点上（有可能是一条直线，有可能是一个平面…… ）。

变换后落在原点的向量的集合，被称为矩阵的零空间或者核（kernel）。

对于二维线性方程组来说，零空间给出的就是这个向量方程所有可能的解！

非方阵

非方阵的几何意义。

例如我们先来考虑一个二维向量到三维向量的变换。

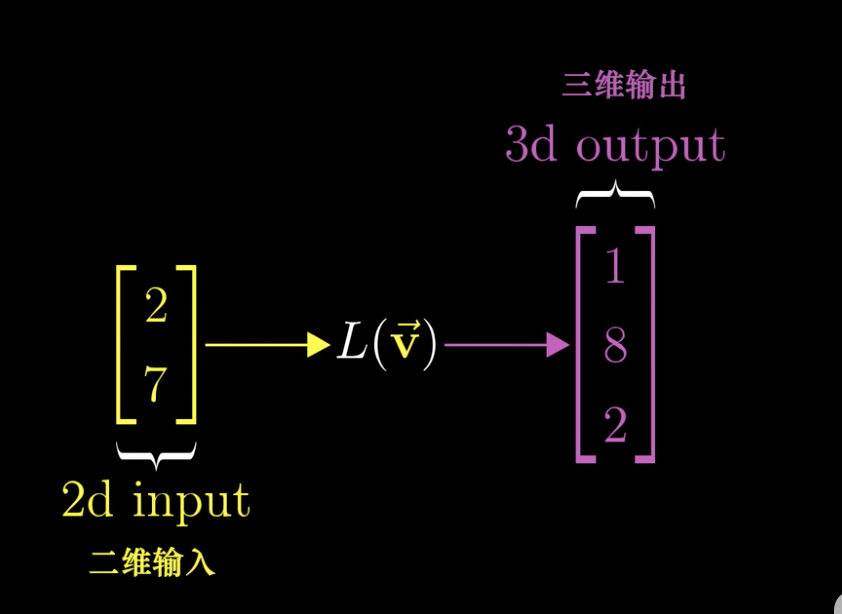
和之前一样，如果网格线保持平行且等距分布，并且原点映射为自身，就称它为线性的。

其实也就是基向量的变化，例如

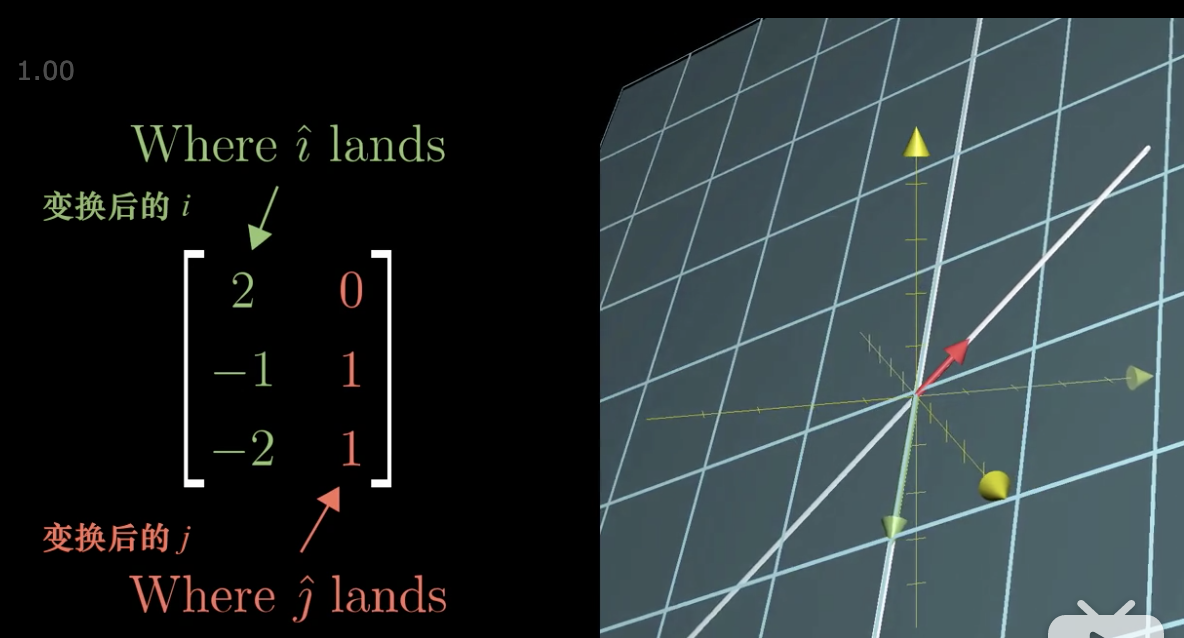
i和j 都变化了，我们只需要按照之前的变换方式就可以计算出变换后的向量了。

而这个 3x2 的矩阵，他们张成的列空间为一个过原点的平面。但是这个矩阵仍然是满秩的。

也就是把二维空间映射到三维空间中，每个基向量在变换后都有对应的基向量。

同样，一个 2x3 的矩阵就可以从三维空间映射到二维空间中。

一个 1x2 的矩阵就可以把平面上的点映射到了数轴上。

这样，矩阵和行列式的理解，就更深了一步。

继续加油。