五大算法之回溯算法

Posted 2021-03-02 bobpong

        回溯算法是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

        回溯法解决的问题可以用树结构来描述，每个状态下都对应有n种选择。以全排列问题为例，如对[1, 2, 3]进行全排列，每次从1, 2, 3中选择了一个值后，下一次又可以从1, 2, 3中选择一个值，将这个过程绘制成一棵树，每个节点都有1, 2, 3三个子节点。通常对树的遍历为深度优先的方式，即先序遍历的方式，如果遍历整个树结构，那么时间复杂度将是指数级的，回溯法则通过一定的条件判断，当节点不满足条件时，就会回退到上一个节点，然后再开始下一次的遍历，从而对树进行剪枝，减少需要遍历的路径。如排列的结果无重复值，这一回溯条件可减去多余的路径，同时回溯法还有终止条件，如排列结果长度为3。

 

 

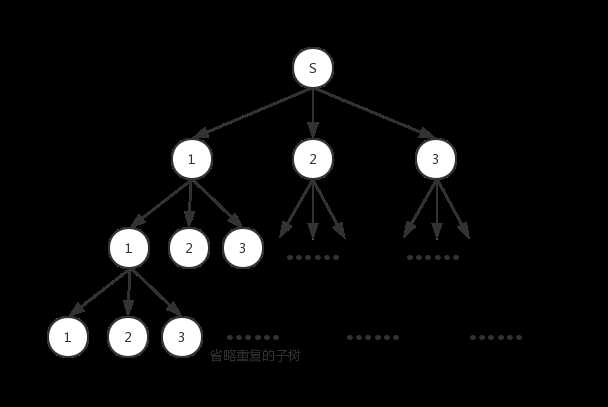
因此，解决一个回溯问题，实际上就是一个决策树的遍历过程。有四个要素需要考虑：

• 当前路径：指的是已经做出的选择。
• 选择列表：指的是当前所有可做的选择。
• 回溯条件：指的是判断选择是否有效。
• 终止条件：指的是到达决策树底层，无法再做选择的条件。

代码方面，回溯算法的框架如下，其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」。

result = []
def backtrack(当前路径, 选择列表):
    if 满足终止条件:
        result.add(路径)
        return

for 选择 in 选择列表:
        if 选择满足回溯条件：
            做选择
            backtrack(当前路径, 选择列表)
            撤销选择

 

一、全排列问题

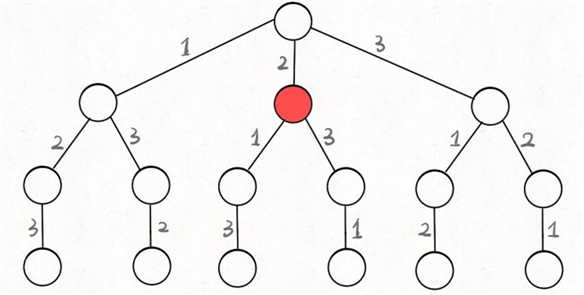
        下面还是以全排列为例，在红色节点状态时，当前路径为[2]，可选择的数字是[1,2,3]，但是满足回溯条件即无重复值的只有[1,3]，终止条件为全排列结果长度为3。

代码如下：

class Solution {
public:
    vector<vector<int>> res;
    vector<vector<int>> permute(vector<int>& nums) {
        vector<int> tmp;
        backtrack(tmp,nums);
        return res;
    }
    void backtrack(vector<int> tmp,vector<int> nums)
    {
        if(tmp.size() == nums.size())
        {
            res.push_back(tmp);
            return;
        }
        for(int i=0;i<nums.size();i++)
        {
            vector<int>::iterator iter;
            iter = std::find(tmp.begin(),tmp.end(),nums[i]);
            if(iter==tmp.end())
            {
                tmp.push_back(nums[i]);
                backtrack(tmp,nums);
                tmp.pop_back();
            }
        }
    }
};

         至此，我们就通过全排列问题详解了回溯算法的底层原理。当然，这个算法解决全排列不是很高效，因为对vector使用find需要 O(N) 的时间复杂度。有更好的方法通过交换元素达到目的。但是必须说明的是，不管怎么优化，都符合回溯框架，而且时间复杂度都不可能低于O(N!)，因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点，不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高。

 

二、括号生成问题

        给出n代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。例如，给出n = 3，生成结果为：["((()))", "(()())", "(())()", "()(())", "()()()"]。

合法括号组合满足一下两点条件：

• 一个合法括号组合的左括号数一定等于右括号数，这个显而易见。
• 一个合法括号组合生成过程中，左括号生成数一定大于等于右括号生成数。比如这个括号组合"))(("，前几个子串都是右括号多于左括号，显然不是合法的括号组合。

 

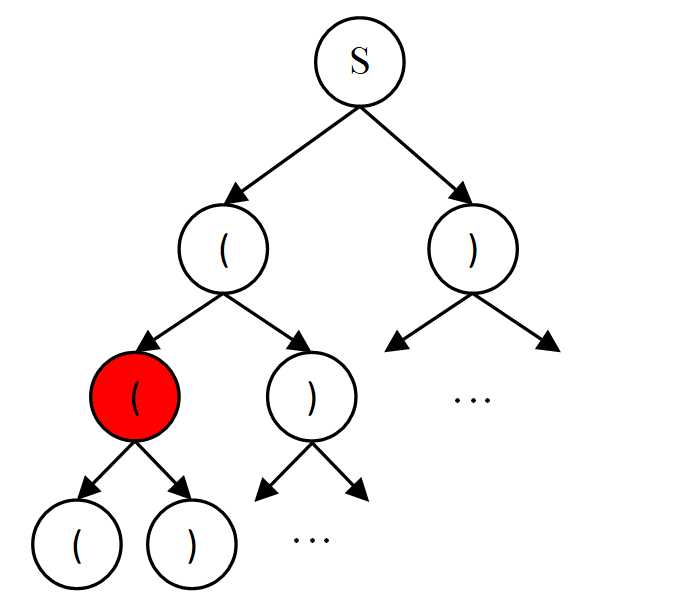
        根据上述的回溯法四个要素，我们逐个分析，对于红色节点，当前路径为“((”；可选择的数字是[‘(’, ‘)’]；回溯条件为：左括号数小于等于n，右括号生成数小于等于左括号数；终止条件为：总括号生成数等于n*2。代码如下：

class Solution {
public:
    vector<string> res;
    int left = 0;
    int right = 0;
    
    vector<string> generateParenthesis(int n) {
        backtrace("",n);
        return res;
    }
    
    void backtrace(string tmp,int n)
    {
        if(tmp.size()==n*2) 
        {
            res.push_back(tmp);
            return;
        }

        if(left < n)
        {
            tmp.push_back(‘(‘);
            left++;
            backtrace(tmp,n);
            tmp.pop_back();
            left--;
        }
        if(right<left)
        {
            tmp.push_back(‘)‘);
            right++;
            backtrace(tmp,n);
            tmp.pop_back();
            right--;
        }
    }
};