数论小模块——矩阵运算的那些事

Posted 2020-11-13 rr-jin

P3390 【模板】矩阵快速幂

1.　　矩阵A的大小为 n×m，B的大小为 n×k，设C=A×B

　　　　 有公式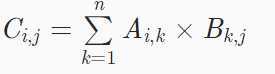 

　　　　引用机房大佬一句很不错的总结：第一个矩阵的x行*第二个矩阵的y列，结果相加，作为结果矩阵的(x行，y列)处的数。

 

               Eg: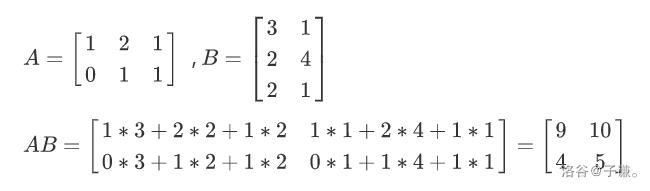 　　

2.　　 矩阵乘满足结合律：(AB)C = A(BC)

3. 　　单位矩阵：它从左上角到右下角的对角线上的元素均为1，除此以外全都为0。

                             它在矩阵乘中相当于数乘中的1，即任何矩阵乘它都等于本身。

 

 1 #include<cstdio>
 2 #include<cstring>
 3 #define ll long long
 4 const ll mod = 1e9+7;
 5 const int N = 110;
 6 using namespace std;
 7 int n;
 8 ll k;
 9 struct node{
10     ll m[N][N];
11 };
12 node a,e;
13 node mul(node x,node y){        //两个矩阵相乘 
14     node c;
15     for(int i=1;i<=n;i++)
16         for(int j=1;j<=n;j++)
17             c.m[i][j]=0;        //注意初始化 
18     for(int i=1;i<=n;i++)
19         for(int j=1;j<=n;j++)
20             for(int k=1;k<=n;k++)
21                 c.m[i][j]=(c.m[i][j]+x.m[i][k]*y.m[k][j]%mod)%mod;    //公式 
22     return c;
23 }    
24 void ksm(node x,ll y){        //矩阵快速幂 
25     while(y){
26         if(y&1) e=mul(e,x);
27         x=mul(x,x);
28         y>>=1;
29     }
30 }
31 int main()
32 {
33     scanf("%d%lld",&n,&k);
34     for(int i=1;i<=n;i++)
35         for(int j=1;j<=n;j++)
36             scanf("%lld",&a.m[i][j]);
37     for(int i=1;i<=n;i++) e.m[i][i]=1;        //单位矩阵 
38     ksm(a,k);
39     for(int i=1;i<=n;i++){
40         for(int j=1;j<=n;j++)
41             printf("%lld ",e.m[i][j]%mod);
42         printf("
");
43     }
44     return 0;
45 }

 
P1939【模板】矩阵加速（数列）

　　1.　　又圆润地去学习了一下矩阵构造 https://www.cnblogs.com/frog112111/archive/2013/05/19/3087648.html

 

 1 #include<cstdio>
 2 #include<cstring>
 3 using namespace std;
 4 const int mod=1e9+7;
 5 int T;
 6 long long n;
 7 struct node{
 8     long long m[5][5];        //注意开long long,否则中间运算会爆掉 
 9 };
10 node A,f,e;
11 node mul(node x,node y){
12     node c;
13     memset(c.m,0,sizeof(c.m));
14     for(int i=1;i<=3;i++)
15         for(int j=1;j<=3;j++)
16             for(int k=1;k<=3;k++)
17                 c.m[i][j]=(c.m[i][j]+x.m[i][k]*y.m[k][j]%mod)%mod;
18     return c;
19 }
20 void ksm(node x,long long y){
21     while(y){
22         if(y&1) e=mul(e,x);
23         x=mul(x,x);
24         y>>=1;
25     }
26 } 
27 int main()
28 {
29     scanf("%d",&T);
30     memset(A.m,0,sizeof(A.m));        //结构体数组memset~ 
31     A.m[1][3]=A.m[2][1]=A.m[3][2]=A.m[3][3]=1;
32     while(T--){
33         f.m[1][1]=f.m[1][2]=f.m[1][3]=1;
34         memset(e.m,0,sizeof(e.m));
35         for(int i=1;i<=3;i++) e.m[i][i]=1;
36         scanf("%lld",&n);
37         if(n==1||n==2||n==3){         //注意特判(x!=n) 
38             printf("%d
",1);
39             continue;
40         }
41         ksm(A,n-3);        //基础矩阵快速幂 
42         f=mul(f,e);
43         printf("%d
",f.m[1][3]%mod);
44     }    
45     return 0;
46 }

　　2.　　 就着这道题又水了一题　　P1962 斐波那契数列

 

 1 #include<cstdio>
 2 #include<cstring>
 3 using namespace std;
 4 const int mod=1e9+7;
 5 long long n;
 6 struct node{
 7     long long m[5][5];        //注意开long long,否则中间运算会爆掉 
 8 };
 9 node A,f,e;
10 node mul(node x,node y){
11     node c;
12     memset(c.m,0,sizeof(c.m));
13     for(int i=1;i<=3;i++)
14         for(int j=1;j<=3;j++)
15             for(int k=1;k<=3;k++)
16                 c.m[i][j]=(c.m[i][j]+x.m[i][k]*y.m[k][j]%mod)%mod;
17     return c;
18 }
19 void ksm(node x,long long y){
20     while(y){
21         if(y&1) e=mul(e,x);
22         x=mul(x,x);
23         y>>=1;
24     }
25 } 
26 int main()
27 {
28     A.m[1][1]=0; 
29     A.m[1][2]=A.m[2][1]=A.m[2][2]=1;
30     f.m[1][1]=f.m[1][2]=1;
31     memset(e.m,0,sizeof(e.m));
32     for(int i=1;i<=2;i++) e.m[i][i]=1;
33     scanf("%lld",&n);
34     ksm(A,n-1);        //基础矩阵快速幂 
35     f=mul(f,e);
36     printf("%d
",f.m[1][1]%mod);
37     return 0;
38 }