二叉树

Posted 2021-03-01 java0120

树形结构

• 树结构基本概念：
  节点、根节点、父节点、子节点、兄弟节点、子树、左子树、右子树；
  空树：没有任何节点的树；

• 节点的度：子树的个数

• 树的度：所有节点度中的最大值（max）

• 叶子节点：度为0的节点

• 非叶子节点：度不为0的节点

• 层数：根节点在第一层，根节点的子节点在第二层，以此类推

• 节点的深度：从根节点到当前节点的唯一路径上的节点总数

• 节点的高度：从当前节点到最远叶子节点的路径上的节点总数

• 树的深度：所有节点深度中的最大值

• 树的高度：所有节点高度中的最大值

• 树的高度==树的深度

分类：

• 有序树：树中任意节点的子节点之间有顺序关系
• 无序树：树中任意节点的子节点之间没有顺序关系（自由树）

二叉树（Binary Tree）

特点：

• 每个节点的度最大为2（最多拥有两个子树）
• 左子树和右子树是顺序的
• 即使某节点只有一个子树，也要区分左右子树
  例子：
  
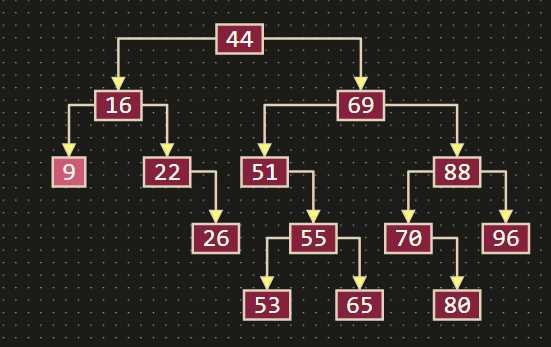
  二叉树是有序树

性质：

• 非空二叉树的第i层，最多有2^（i-1）个节点（i>=1）
• 在高度为h的二叉树上最多有2^h - 1个节点（h>=1）
• 对于任意非空二叉树，如果叶子节点个数为n0，度为2的节点个数为n2，则有：n0 = n2 + 1
  推论：
  1. 假设度为1的节点个数为n1，那么二叉树的节点总数n = n0+n1+n2
  2. 二叉树的边数T = n1 + 2*n2 = n - 1 = n0+n1+n2-1
  3. 因此n0 = n2+1

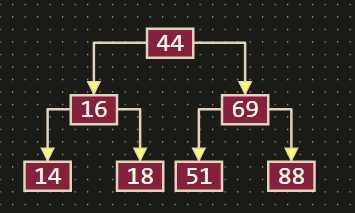
真二叉树（Proper Binary Tree）

• 所有节点的度都为0或者2
  示例：
  

满二叉树（Full Binary Tree）

性质：

• 最后一层节点的度都为0，其他节点的度都为2
• 在同样高度的二叉树中，满二叉树的叶子节点数量最多、总节点数量最多
• 满二叉树一定是真二叉树，真二叉树不一定是满二叉树
• 假设满二叉树的高度为h（h>=1），那么：
  1. 第i层的节点数量：2^(i-1)
  2. 叶子节点数量：2^(h-1)
  3. 总节点数量n与高度h关系：n = 2^h - 1 h = log2(n+1)
  示例：
  

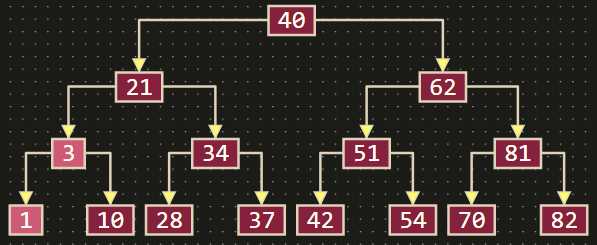
完全二叉树（Complete Binary Tree）

定义：从节点从上至下，左至右开始编号，其所有编号都能与相同高度的满二叉树中的编号对应

• 叶子节点只会出现在最后两层，最后一层的叶子节点都靠左对齐
• 完全二叉树从根节点至倒数第二层是一颗满二叉树
• 满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树
• 度为1的节点只有左子树
• 度为1的节点要么是1个，要么是0个
• 同样节点数量的二叉树，完全二叉树的高度最小
• 假设完全二叉树的高度为h（h>=1），那么
  1. 至少有2^（h-1）个节点
  2. 最多有2^h - 1个节点（此时也为满二叉树）
  3. 总节点数量n与h关系：2^（h-1）<= n <=2^h h-1<= log2n <h h = floor(log2n) + 1(floor是向下取整，ceiling是向上取整)
• 一颗有n个节点的完全二叉树(n>0)，从上至下，左至右对节点从1开始编号，对任意第i个节点
  1. 如果i = 1，它是根节点
  2. 如果i > 1，它的父节点编号为floor（i/2）
  3. 如果2i <= n， 它的左子节点编号为2i
  4. 如果2i > n，它无左子节点
  5. 如果2i + 1 <= n，它的有子节点编号为2i+1
  6. 如果2i + 1 > n，它无右子节点
• 一颗有n个节点的完全二叉树(n>0)，从上至下，左至右对节点从0开始编号，对任意第i个节点
  1. 如果i = 1，它是根节点
  2. 如果i > 1，它的父节点编号为floor（（i-1）/2）
  3. 如果2i + 1 <= n - 1， 它的左子节点编号为2i+1
  4. 如果2i + 1 > n -1，它无左子节点
  5. 如果2i + 2 <= n - 1，它的有子节点编号为2i+2
  6. 如果2i + 2 > n - 1，它无右子节点

题目：

假如有一颗完全二叉树有768个节点，求叶子节点的个数
解：假设叶子节点个数为n0，度为1的节点个数为n1，度为2的节点个数为n2（n=2n0+n1-1）.
又因为完全二叉树的n1要么为1，要么为0. n1为1时，n=2n0，n必然为偶数，则叶子节点n0 = n/2. n1为0时，n=2n0 - 1， n必然是奇数， 则叶子节点n0 = （n+1）/2。
总结：叶子节点n0 = floor（（n+1）/2） = ceiling（n/2） 非叶子节点n1+n2 = floor（n/2） = ceiling（（n-1）/2）.
所以此题的叶子节点个数为384.

二叉树的遍历

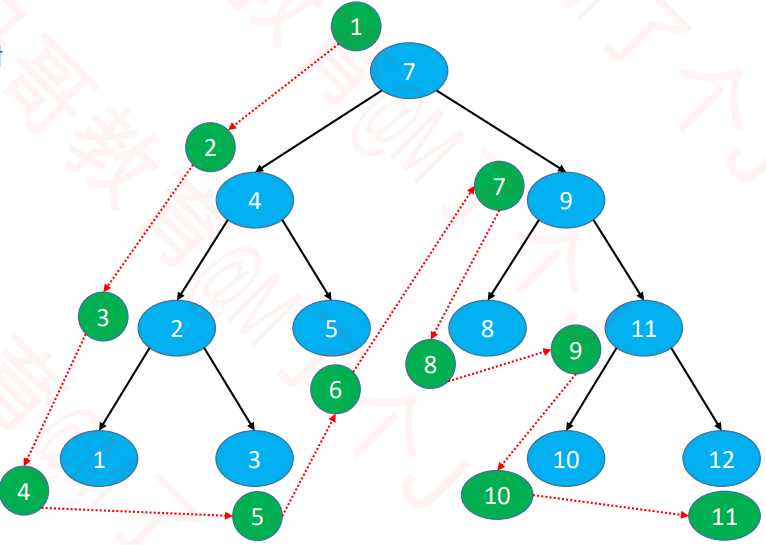
• 前序遍历（Preorder Traversal）
  访问顺序：根节点，前序遍历左子节点，前序遍历右子节点
  示图：
  
  前序遍历代码：

//递归实现前序遍历
public void preorder(Visitor<E> visitor) {
	if (visitor == null) return;
	preorder(root, visitor);
}
private void preorder(Node<E> node, Visitor<E> visitor) {
	if (node == null || visitor.stop) return;
	
	visitor.stop = visitor.visit(node.element);
	preorder(node.left, visitor);
	preorder(node.right, visitor);
}

/**
 * 前序遍历（非递归遍历）(使用Stack实现)
 * @param visitor
 */
public void preorder(Visitor<E> visitor) {
	if (visitor == null || root == null) return;
	Stack<Node<E>> stack = new Stack<>();
	stack.push(root);//将根节点入栈
	while (!stack.isEmpty()){//栈不空执行while循环
		Node<E> node = stack.pop();//取出栈顶节点
		//访问node节点
		if (visitor.visit(node.element)) return;
		//node的右子节点不为空时，右子节点入栈
		if (node.right != null) stack.push(node.right);
		//node的左子节点不为空时，左子节点入栈
		if (node.left != null) stack.push(node.left);
	}
}
//前序遍历方式二（非递归遍历）(使用Stack实现)
public void preorder2(Visitor<E> visitor) {
	if (visitor == null || root == null) return;
	Node<E> node = root;
	Stack<Node<E>> stack = new Stack<>();
	while (true){
		if (node != null){
			//访问node节点
			if (visitor.visit(node.element)) return;
			//将右子节点入栈
			if (node.right != null) stack.push(node.right);
			//向左走
			node = node.left;
		} else {
			//若栈空了，便结束方法
			if (stack.isEmpty()) return;
			//处理右边节点
			node = stack.pop();
		}
	}
}

• 中序遍历（Inorder Traversal）
  访问顺序：中序遍历左子节点，根节点，中序遍历右子节点（遍历二叉搜索树时，节点值是有序的）
  示图：
  
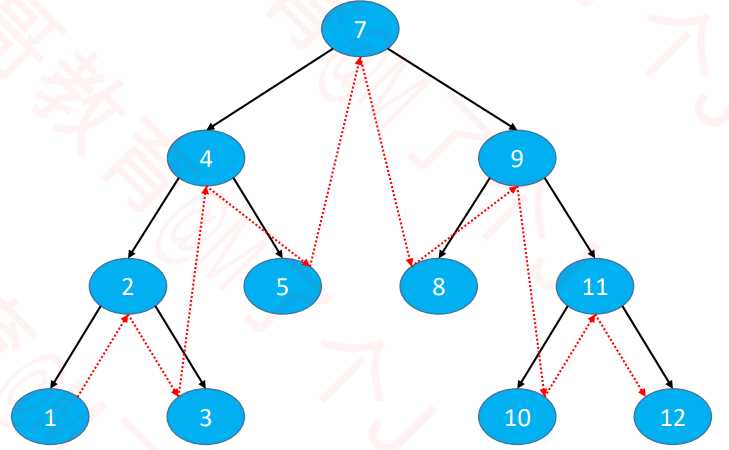
  中序遍历代码：

//递归方式实现中序遍历
public void inorder(Visitor<E> visitor) {
	if (visitor == null) return;
	inorder(root, visitor);
}
private void inorder(Node<E> node, Visitor<E> visitor) {
	if (node == null || visitor.stop) return;
	
	inorder(node.left, visitor);
	if (visitor.stop) return;
	visitor.stop = visitor.visit(node.element);
	inorder(node.right, visitor);
}

/**
 * 中序遍历（非递归遍历）(使用Stack实现)
 * @param visitor
 */
public void inorder(Visitor<E> visitor) {
	if (visitor == null || root == null) return;
	Node<E> node = root;
	Stack<Node<E>> stack = new Stack<>();
	while (true){
		if (node != null){
			stack.push(node);
			//向左走
			node = node.left;
		} else {
			//若栈空了，便结束方法
			if (stack.isEmpty()) return;
			node = stack.pop();
			//访问node节点
			if (visitor.visit(node.element)) return;
			//让右节点进行中序遍历
			node = node.right;
		}
	}
}

• 后序遍历（Postorder Traversal）
  访问顺序：后序遍历左子节点，后序遍历右子节点，根节点
  示图：
  
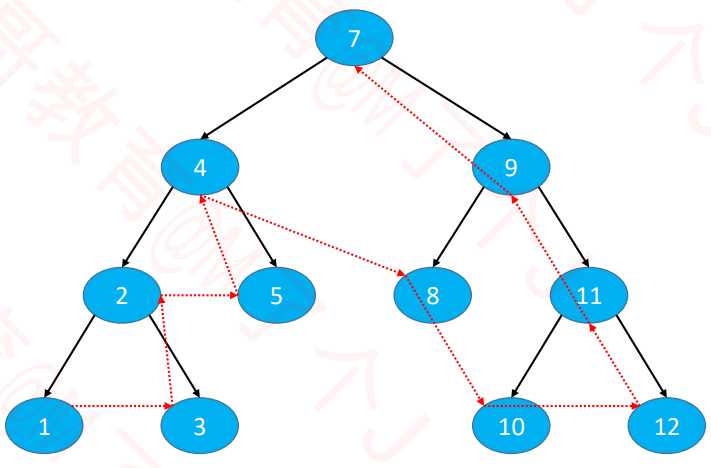
  后序遍历代码：

//递归方式实现后序遍历
public void postorder(Visitor<E> visitor) {
	if (visitor == null) return;
	postorder(root, visitor);
}
private void postorder(Node<E> node, Visitor<E> visitor) {
	if (node == null || visitor.stop) return;
	
	postorder(node.left, visitor);
	postorder(node.right, visitor);
	if (visitor.stop) return;
	visitor.stop = visitor.visit(node.element);
}

/**
 * 后序遍历（非递归遍历）(使用Stack实现)
 * @param visitor
 */
public void postorder(Visitor<E> visitor) {
	if (visitor == null || root == null) return;
	//记录上一次弹出访问的节点
	Node<E> prev = null;
	Stack<Node<E>> stack = new Stack<>();
	while (!stack.isEmpty()){
		Node<E> top = stack.peek();//获取栈顶节点,但并不取出栈顶节点
		//若栈顶元素为叶子节点或者栈顶元素为上一个弹出元素的子节点，则执行
		if (top.isLeaf() || (prev != null && prev.parent == top)){
			prev = stack.pop();
			//访问节点
			if (visitor.visit(prev.element))return;
		} else {
			if (top.right != null) stack.push(top.right);
			if (top.left != null) stack.push(top.left);
		}
	}
}

• 层序遍历（Level ORder Traversal）
  访问顺序：从上到下，从左到右依次访问每一个节点（用于计算二叉树高度或判断是否为完全二叉树）
  示图：
  
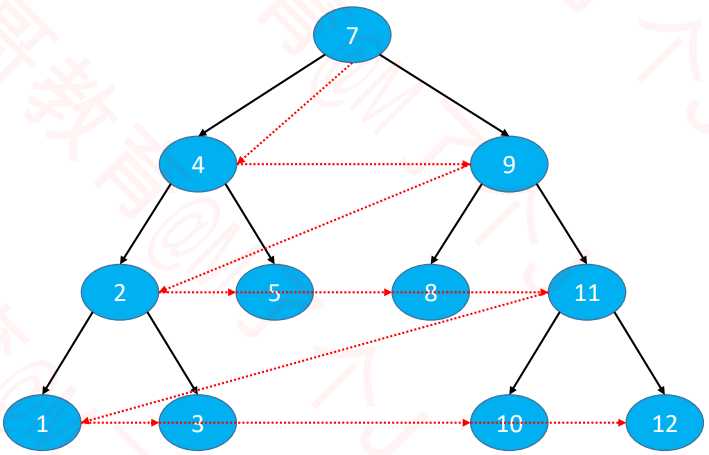
  层序遍历代码：

public void levelOrder(Visitor<E> visitor) {
	if (root == null || visitor == null) return;
	
	Queue<Node<E>> queue = new LinkedList<>();
	queue.offer(root);
	
	while (!queue.isEmpty()) {
		Node<E> node = queue.poll();
		if (visitor.visit(node.element)) return;
		
		if (node.left != null) {
			queue.offer(node.left);
		}
		
		if (node.right != null) {
			queue.offer(node.right);
		}
	}
}

前驱节点（predecessor）

定义：中序遍历时的前一个节点（如果说二叉搜索树，前驱节点就是前一个比它小的节点）
代码实现：

/**
 * 前驱节点:中序遍历时，某节点的前一个节点
 * 求前驱节点
 * @param node
 * @return 前驱节点
 */
private Node<E> predecessor(Node<E> node){
    if (node == null) return null;

    //从当前节点的左子树中寻找前驱节点(node.left.right.right...)
    Node<E> p = node.left;
    if(p != null){
        //获取到左子树最右的节点
        while (p.right != null) {
            p = p.right;
        }
        return p;
    }

    //从父节点||祖父节点中寻找前驱节点(node.parent.parent...)
    //终止条件:当前节点为父节点的右子树，此时的父节点就是前驱节点
    while (node.parent != null && node == node.parent.left){
        node = node.parent;
    }
    /**
     * 到达此处的代码符合的条件为
     * node.parent == null;
     * node == node.parent.right
     */
    return node.parent;
}

后继节点（successor）

定义：中序遍历时的后一个节点（如果说二叉搜索树，后继节点就是后一个比它大的节点）
代码实现：

/**
 * 后继节点:中序遍历时，某节点的后一个节点
 * 求后继节点
 * @param node
 * @return 后继节点
 */
private Node<E> successor(Node<E> node){
    if (node == null) return null;

    //从当前节点的右子树中寻找后继节点(node.right.left.left...)
    Node<E> p = node.right;
    if(p != null){
        //获取到右子树最左的节点
        while (p.left != null) {
            p = p.left;
        }
        return p;
    }
    //从父节点||祖父节点中寻找后继节点(node.parent.parent...)
    //终止条件:当前节点为父节点的左子树，此时的父节点就是后继节点
    while (node.parent != null && node == node.parent.right){
        node = node.parent;
    }
    return node.parent;
}

判断当前二叉树是否为完全二叉树代码：

    //层序遍历二叉树（用队列）
    public boolean isComplete(){
        if (root == null) return false;

        Queue<Node<E>> queue = new LinkedList<>();
        queue.offer(root);
        boolean leaf = false;//节点是否为叶子节点
        while (!queue.isEmpty()){
            Node<E> node = queue.poll();
            //如果当前节点在应该为叶子节点时，不为叶子节点，那此二叉树不是完全二叉树
            if(leaf && !node.isLeaf()) return false;

            if (node.left != null){
                queue.offer(node.left);
            } else if (node.right != null){
                //左子节点为i空，右子节点不为空，此树不为完全二叉树
                return false;
            }
            if (node.right != null){
                queue.offer(node.right);
            } else {
                //左子节点可能为空,可能不空,但右子节点一定为空
                //此时的节点应该为叶子节点
                leaf = true;
            }
        }
        return true;
    }