树的深度———树形DP

Posted 2021-03-01 liuchanglc

题目描述

 

 输入

 

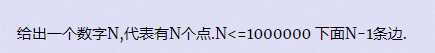
 输出

 

 样例

样例输入

8
1 4
5 6
4 5
6 7
6 8
2 4
3 4

View Code

样例输出

7

分析

这道题数据有1000000，把每一个顶点都枚举一次显然不现实，肯定会T掉

所以，我们还是从图中找规律

按照习惯，我们先把1号节点作为根节点模拟一下

 

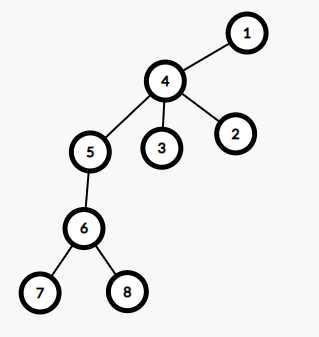
 我们可以很容易的通过一次dfs求出1号节点作为根节点时树的深度之和

1+2*3+3+4*2=18（当然，你把根节点的深度置为1也不会影响结果）

那么我们把根节点向下移到4好节点，我们可以发现什么呢

这时同把1作为根节点相比，1号节点的深度增加了1，但4所在的子树的节点的深度都减小了1

同样地，我们再把根节点下移到5，这时同把4作为根节点相比，1、4、3、2号节点的深度增加了1，但5所在的子树的节点的深度都减小了1

所以，我们设ans[i]为以i作为根节点时树的度数之和，siz[i]为以i为根子树的大小

那么ans[i]=ans[fa]+n-siz[i]+siz[i]=ans[fa]+n-2*siz[i]

siz数组我们可以预处理得到，ans[fa]我们也可以由ans[1]求得，所以，这道题就迎刃而解了

代码

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 #include<iostream>
 5 #include<cmath>
 6 using namespace std;
 7 const int maxn=2000010;
 8 typedef long long ll;
 9 struct asd{
10     ll from,to,next;
11 }b[maxn];
12 ll head[maxn],tot=1,n;
13 void ad(ll aa,ll bb){
14     b[tot].from=aa;
15     b[tot].to=bb;
16     b[tot].next=head[aa];
17     head[aa]=tot++;
18 }
19 ll dep[maxn],ans[maxn],siz[maxn];
20 void dfs(ll now,ll fa){
21     dep[now]=dep[fa]+1;
22     siz[now ]=1;
23     ans[now]=dep[now];
24     for(ll i=head[now];i!=-1;i=b[i].next){
25         ll u=b[i].to;
26         if(u==fa) continue;
27         dfs(u,now);
28         siz[now]+=siz[u];
29         ans[now]+=ans[u];
30     }
31 }
32 void dfs2(ll now,ll fa){
33     for(ll i=head[now];i!=-1;i=b[i].next){
34         ll u=b[i].to;
35         if(u==fa) continue;
36         if(u!=1){
37             ans[u]=ans[now]+(n-siz[u])-siz[u];
38         }
39         dfs2(u,now);
40     }
41 }
42 int main(){
43     memset(head,-1,sizeof(head));
44     scanf("%lld",&n);
45     for(ll i=1;i<n;i++){
46         ll aa,bb;
47         scanf("%lld%lld",&aa,&bb);
48         ad(aa,bb);
49         ad(bb,aa);
50     }
51     dep[0]=-1;//也可以置为0，都可以
52     dfs(1,0);
53     dfs2(1,0);
54     ll tot=-1,jll=1;
55     for(ll i=1;i<=n;i++){
56         if(ans[i]>tot){
57             tot=ans[i];
58             jll=i;
59         }
60     }
61     printf("%lld
",jll);
62     return 0;
63 }

View Code