DFS序常见用法及代码实现

Posted 2021-03-01 hznudreamer

dfs序就是一棵树在dfs遍历时组成的节点序列.

它有这样一个特点:一棵子树的dfs序是一个区间. 下面是dfs序的基本代码:

 1 void dfs(int x,int pre,int d){//L,R表示一个子树的范围
 2     L[x]=++tot;
 3     dep[x]=d;
 4     for(int i=0;i<e[x].size();i++){
 5         int y=e[x][i];
 6         if(y==pre)continue;
 7         dfs(y,x,d+1);
 8     }
 9     R[x]=tot;
10 }

给定一颗树, 和每个节点的权值.下面有7个经典的关于dfs序的问题:

下面所有问题都采用如图的树作为样例

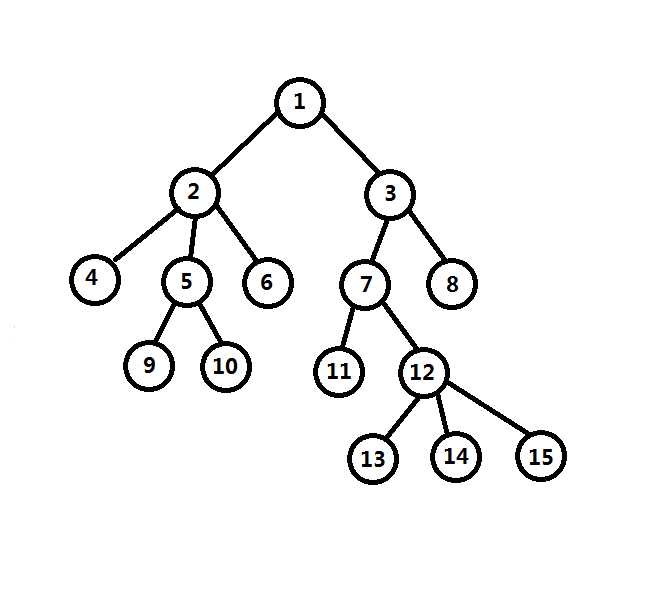
都有以下初始化建树代码：

 1 const int n = 15;
 2 const int maxn = 1010;
 3 struct E{
 4     int to,next;
 5 }edge[maxn];
 6 int head[maxn], cnt;
 7 int t[maxn];
 8 inline void addedge(int u,int v){
 9     edge[cnt] = (E){v,head[u]};
10     head[u] = cnt++;
11     edge[cnt] = (E){u,head[v]};
12     head[v] = cnt++;
13 }
14 void build(){
15     memset(head, -1, sizeof head);
16     int tmp[28] = {1,2,1,3,2,4,2,5,2,6,3,7,3,8,5,9,5,10,7,11,7,12,12,13,12,14,12,15};
17     for (int i = 0; i < 14*2; i+=2){
18         addedge(tmp[i],tmp[i+1]);
19     }
20 }

 

1.对某个节点X权值加上一个数W, 查询某个子树X里所有点权的和.

由于X的子树在DFS序中是连续的一段, 只需要维护一个dfs序列,用树状数组实现:单点修改和区间查询.

代码实现：

 1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 
 6 const int n = 15;
 7 const int maxn = 1010;
 8 struct E{
 9     int to,next;
10 }edge[maxn];
11 int head[maxn], cnt;
12 int t[maxn];
13 inline void addedge(int u,int v){
14     edge[cnt] = (E){v,head[u]};
15     head[u] = cnt++;
16     edge[cnt] = (E){u,head[v]};
17     head[v] = cnt++;
18 }
19 void build(){
20     memset(head, -1, sizeof head);
21     int tmp[28] = {1,2,1,3,2,4,2,5,2,6,3,7,3,8,5,9,5,10,7,11,7,12,12,13,12,14,12,15};
22     for (int i = 0; i < 14*2; i+=2){
23         addedge(tmp[i],tmp[i+1]);
24     }
25 }
26 
27 
28 int L[maxn], R[maxn], tot; //l[pos]表示子树的根(编号为pos的子树的dfs序号) R[pos]表示子树结尾的点 L[pos] ~ R[pos]表示以pos为根的子树 
29 void dfs(int u,int pre){
30     L[u] = ++tot;
31     for (int i = head[u]; ~i; i = edge[i].next){
32         int v = edge[i].to;
33         if (v == pre) continue;
34         dfs(v,u);
35     }
36     R[u] = tot;
37 }
38 
39 
40 int tree[maxn];
41 int lowbit(int x){return x & -x;}
42 int add(int x,int w){
43     while (x <= n){
44         tree[x] += w;
45         x += lowbit(x);
46     }
47 }//对每个节点x加上w 
48 int sum(int x){
49     int res = 0;
50     while (x > 0){
51         res += tree[x];
52         x -= lowbit(x);
53     }
54     return res;
55 }
56 int query(int x){
57     return sum(R[x]) - sum(L[x]-1);
58 }// 查询编号为x的子树里所有点的权值和 
59 
60 
61 int main(){
62     build();
63     dfs(1,-1);
64     string op; // 输入Q x表示查询编号为x的子树里所有点权值和 Add x w表示在x节点加上w的权值 
65     int x, w;
66     while (cin >> op){
67         if (op == "Q"){
68             cin >> x;
69             cout << query(x) << endl;
70         } else {
71             cin >> x >> w;
72             add(L[x], w);
73         }
74     }
75     return 0;
76 }
77 /*
78 input : 
79 Add 5 1
80 Add 6 1
81 Q 2
82 Add 7 2
83 Add 12 3
84 Add 13 1
85 Q 12
86 Q 3
87 Q 1
88 output : 
89 2
90 4
91 6
92 8
93 */