八大排序之选择类排序

Posted 2021-03-01 yc-l

直接插入排序

• 在有序数组中插入一个元素，可以作为一种排序方法的基础
• 只有一个元素的数组是一个有序数组，对n个元素的数组，可以从第一个元素所构成的单元数组开始，不断实施插入操作
• 插入第二个元素，得到2个元素的有序数组。插入第三个元素，得到3个元素的有序数组
• 如此反复，得到n个元素的有序数组

示例

对序列：6，5，8，4，3，1 进行直接插入排序

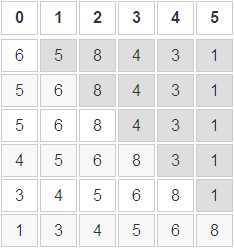
• 图中灰色部分代表待排序列
• 图中透明部分代表已排序列

int main()
{
    int a[10] = { 6,5,8,4,3,7 };

    int temp, j;
    for (int i = 1; i < 6; ++i){
        temp = a[i];
        for (j = i - 1; j >= 0 && temp < a[j]; --j){
            a[j + 1] = a[j];
        }
        a[j + 1] = temp;
    }
    j = 0;
    while (j < 6){
        printf("%d", a[j]);
        ++j;
    }
    return 0;
}

时间复杂度分析

由直接插入排序代码，选取最内层

a[j + 1] = a[j];

作为基本操作语句

1. 考虑最坏的情况，即整个序列是逆序的，O(n^2)
2. 考虑最好的情况，即整个序列是有序的，O(n)

综上所述，本算法的平均时间复杂度O(n^2)

空间复杂度分析

• 算法所需的辅助存储空间不随待排序列规模的变化而变化，是个常量，O(1)

 

折半插入排序

• 与直接插入排序思想类似，区别是查找插入位置的方法不同，折半插入排序是采用折半查找法查找插入位置的
• 将待排序的记录R[i]，通过折半查找的方式在有序序列中查找插入位置

示例

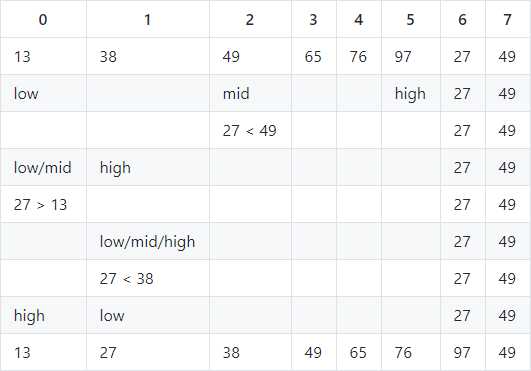
对序列：13，38，49，65，76，97，27，49进行一趟折半插入排序。

前6个元素已经排好序列，查找27的插入位置

1. mid = (0 + 5)/2 = 2，当前位置，27 < 49，27的插入位置在49的低半区
2. h = mid - 1，mid = (0 + 1)/2 = 0，当前位置，27 > 13，27插入位置在13的高半区
3. low = mid + 1，mid = (1 + 1)/2 = 1，27 < 38，27的插入位置在38低半区
4. high = m - 1 = 0，high < low，折半查找结束，27的插入位置在high之后，插入位置后面的元素后移

 

 

 

int main()
{
    // a[0]为存储临时变量的位置
    int a[9] = { 0, 13, 38, 49, 65, 76, 97, 27, 49 };
    int low, high, mid;
    for (int i = 2; i <= 8; ++i){
        a[0] = a[i];
        low = 1;
        high = i - 1;
        while (low <= high){
            mid = (low + high) / 2;
            if (a[mid] > a[0]){
                high = mid - 1;
            }
            else{
                low = mid + 1;
            }                
        }
        for (int j = i - 1; j >= high + 1; --j){
            a[j + 1] = a[j];
        }
        a[high + 1] = a[0];
    }
    int j = 0;
    while (j < 8){
        printf("%d ", a[j]);
        ++j;
    }
    return 0;
}

时间复杂度分析

• 折半插入排序适合关键字数较多的场景，与直接插入排序相比，折半插入排序在查找插入位置上面所花的时间大大减少
• 折半插入排序在关键字移动次数上面和直接插入排序是一样的，所以时间复杂度和直接插入排序还是一样的
• 可知折半插入排序的时间复杂度最好情况为O(nlog2n)，最差情况为O(n^2)，平均情况为O(n^2)

空间复杂度分析

同直接插入排序，O(1)

希尔排序(缩小增量排序)

• 将待排序列分成几个子序列，分别对这几个子序列进行直接插入排序

• 如果增量是1，那么就是直接插入排序

该方法实质上是一种分组插入方法

• 比较相隔较远距离（称为增量）的数，使得数移动时能跨过多个元素，则进行一次比较就可能消除多个元素交换

算法思想

• 先将要排序的一组数按某个增量d分成若干组，每组中记录的下标相差d

• 对每组中全部元素进行排序，然后再用一个较小的增量对它进行，在每组中再进行排序

• 当增量减到1时，整个要排序的数被分成一组，排序完成

示例

• 原始序列：49 38 65 97 76 13 27 45 55 04

• 分割线指向的元素做直接插入排序

void ShellSort(int r[],int n){ 
    int i,j,d;
    int x;
    d=n/2;//d=n>>1
    while(d>=1){
        for(i=d ;i<n;i++){  
            x=r[i];
             for(j=i-d;j>=0;j-=d){
                if(r[j]>x){
                    r[j+d]=r[j];
                }else{
                    break;
                }                
            }               
            r[j+d]=x;
         }//for i
       d>>=1;
      }//while
}//ShellSort

希尔排序不稳定

• 增量序列的最后一个值一定取1

• 增量序列中的值尽量没有除1之外的公因子

时间复杂度

• 时间与步长选取有关，但目前没有对应解析表达式

空间复杂度O(1)