数组问题(鸽巢原理数字交换链表寻环)

Posted 2021-03-01 wjune-0405

287. 寻找重复数

1. 不能更改原数组（假设数组是只读的）。
2. 只能使用额外的 O(1) 的空间。
3. 时间复杂度小于 O(n2) 。
4. 数组中只有一个重复的数字，但它可能不止重复出现一次。

因为不能能改原来的数组，并且只能使用额外O1的空间，所以我们不能使用map记录，也不能维护一个新的数组

因为时间复杂度要在n2以内，所以暴力查找也是不可取的

因为数据范围在1~n-1，所以可以保证不会数组越界，因此使用链表中快慢指针寻找环算法

https://www.cnblogs.com/fankongkong/p/7007869.html

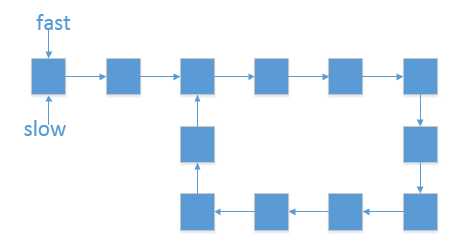
1、当fast指针仅仅只比slow指针多走一个环，如图所示

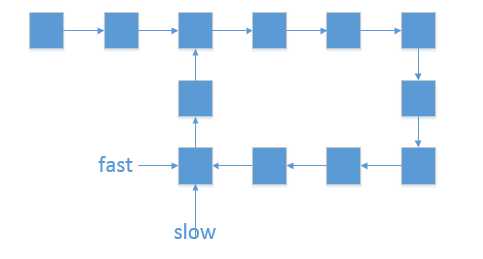
2、第一次相遇的时候，如图

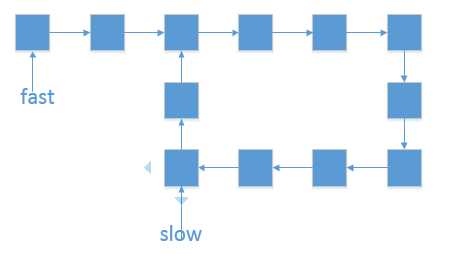
3、这个时候将fast 重新赋值为开头，如图

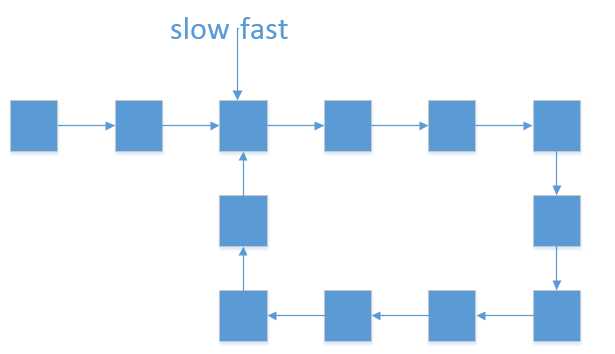
4、再走两次，则找到了环的入口结点

 

重新梳理一下步骤，解题思路

a、第一步，找环中相汇点。分别用fast，slow指向链表头部，slow每次走一步，fast每次走二步，直到fast==slow找到在环中的相汇点。

b、第二步，找环的入口。接上步，当fast==slow时，fast所经过节点数为2x,slow所经过节点数为x,设环中有n个节点，fast比slow多走一圈有2x=n+x; n=x;

可以看出slow实际走了一个环的步数，再让fast指向链表头部，slow位置不变。

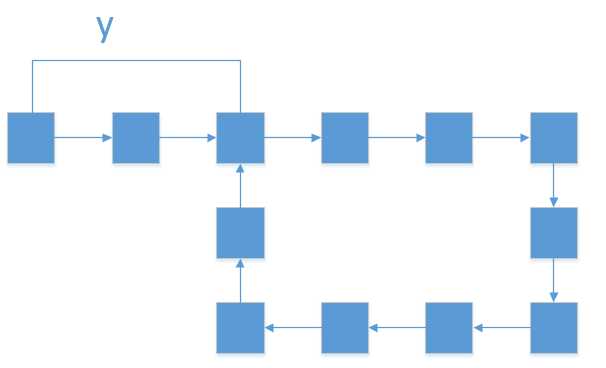
假设链表开头到环接口的距离是y，如下图所示，那么x-y表示slow指针走过的除链表开头y在环中走过的距离，那么slow再走y步，此时fast结点与slow结点相遇，fast == slow ，x-y+y=x = n，即此时slow指向环的入口。

442. 数组中重复的数据

比较好的解法是鸽巢原理+亦或交换数据

不用到任何额外空间并在O(n)时间复杂度

把大小为i的数字，放进下标为i-1的位置上，排完之后还剩下的位置不对的，就是多余的。

对第i位置上的数字k，因为k！=i-1，所以要把k丢到k-1的位置上，然后再看看换过来的数字是不是i-1，不是就继续换（有点像排序算法），当这个位置正确后，就进入下一个位置。

当所有位置处理完以后，再扫一遍，发现位置和数字不匹配的数字就是多余的数字，因为不能采用额外空间，所以使用无额外内存的亦或交换（加减交换也可以）。

public List<Integer> findDuplicates(int[] nums) {
            Set<Integer> res=new HashSet<>();
            for(int i=0;i<nums.length;i++){
                while(nums[i]!=i+1){
                    if(nums[i]==nums[nums[i]-1]){
                        res.add(nums[i]);
                        break;
                    }
                    swap(nums,i,nums[i]-1);
                }
            }

            System.out.println(res.toString());
            return new ArrayList<>(res);
        }
        public void  swap(int[] nums,int a,int b){
            nums[a]^=nums[b];
            nums[b]^=nums[a];
            nums[a]^=nums[b];
        }