[MIT6.006] 11. Integer Arithmetic, Karatsuba Multiplication 整型算术，Karatsuba乘法

Posted 2021-03-01 alvinai

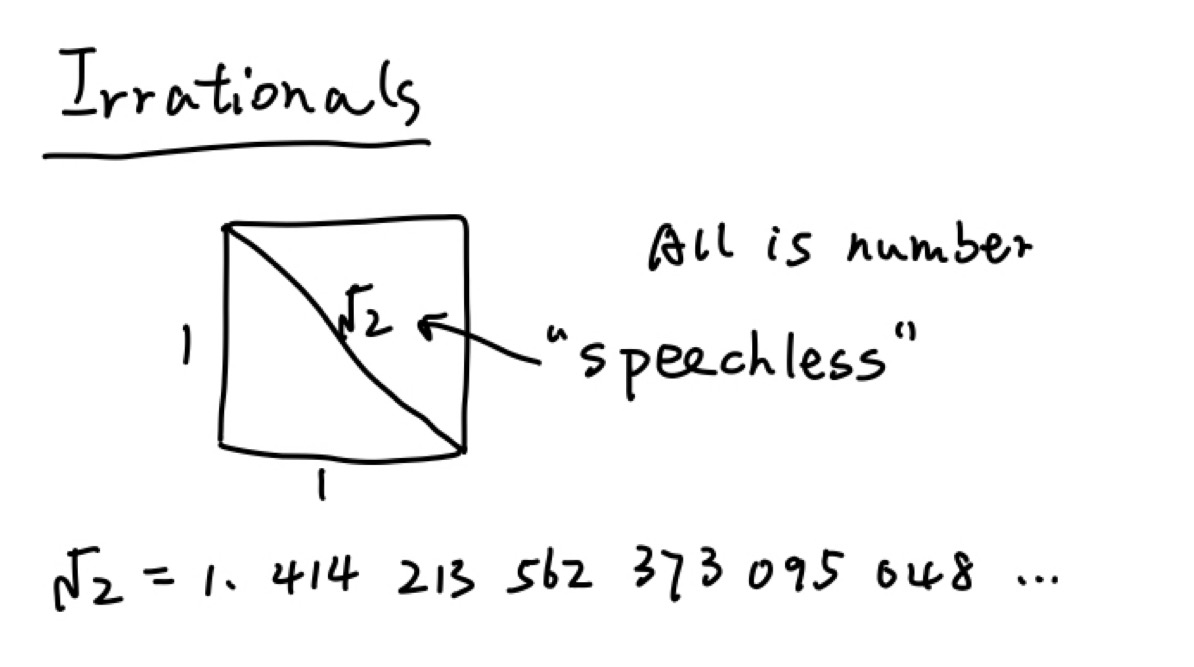
很多人不喜欢√2的表达，他们认为它不是一个数。

 

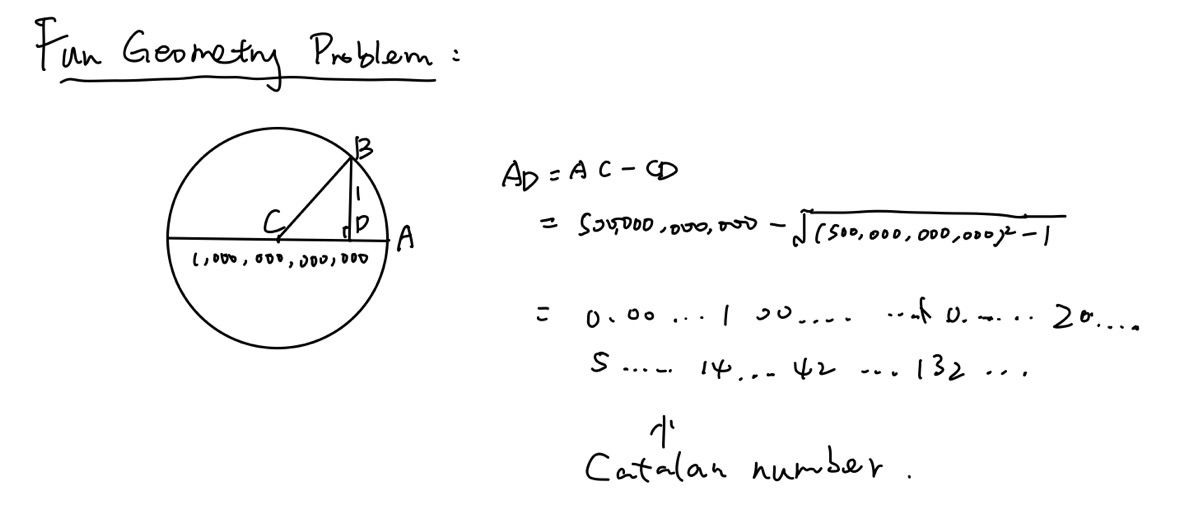
一、卡塔兰数 Catalan numbers

在数方面上，有个著名的数叫卡塔兰数 Catalan numbers，它是组合数学中一个常在各种计数问题中出现的数列。其中它能解决一个叫求括号化方案数量的问题。如图下：

在卡塔兰数下，设P为平衡的父字符串集。

（1）λ属于P集合（λ是空字符串）；

（2）如果α，β都属于P，则（α）β 也属于P。

如果现在有个空字符串（C₀=1）和一对括号（C₁=1），则C₂=C₀C₁ + C₁C₀。归纳结果则为：C_n+1 = ∑C_kC_n-k (n≥0)。

 

关于卡塔兰树的一个有趣集合问题，如下图所示：

 

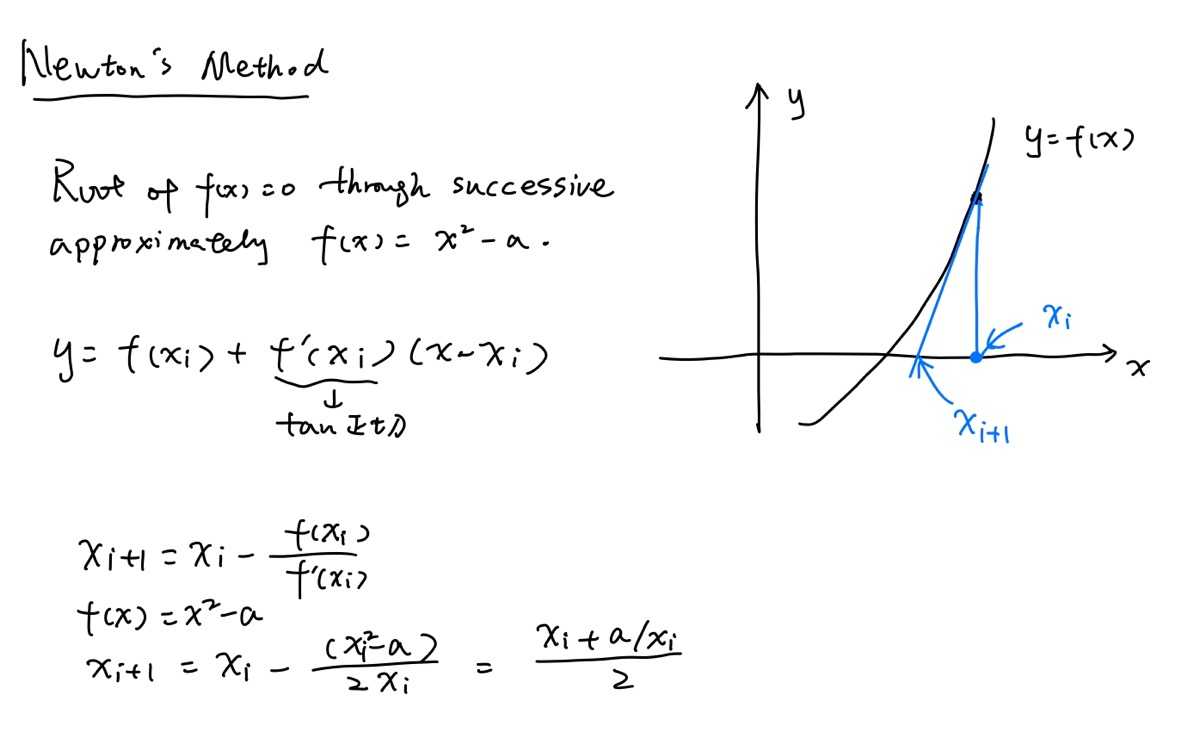
二、牛顿法 Newton‘s Method

牛顿法就是通过不断逼近某函数f(x)来求取f(x)=0的根解。例如下图中f(x) = x² - a。

 

使用牛顿法求解过程中，数的实际精度符合二次收敛（Quadratic convergence）的特性，即梯度双倍增长，如下图：

 

 

 三、高精度乘法

现有两个大数，x，y。首先将x，y分别拆开成为两部分，可得x1，x0，y1，y0。他们的关系如下：

但这种方式的高精度乘法时间上不是最有效率的，最有效率的是下面的Karatsuba算法：