线性时间排序

Posted 2021-02-28 a-runner

　　堆排序，快速排序的时间复杂度为nlog(n)。他们都是运用比较排序的结果。好比决策树模型。

　　属于线性时间排序的算法有：计数排序，基数排序和桶排序。

计数排序：

 

先分别求出每个元素的频数，不过如果元素值较大时，比较浪费内存空间。

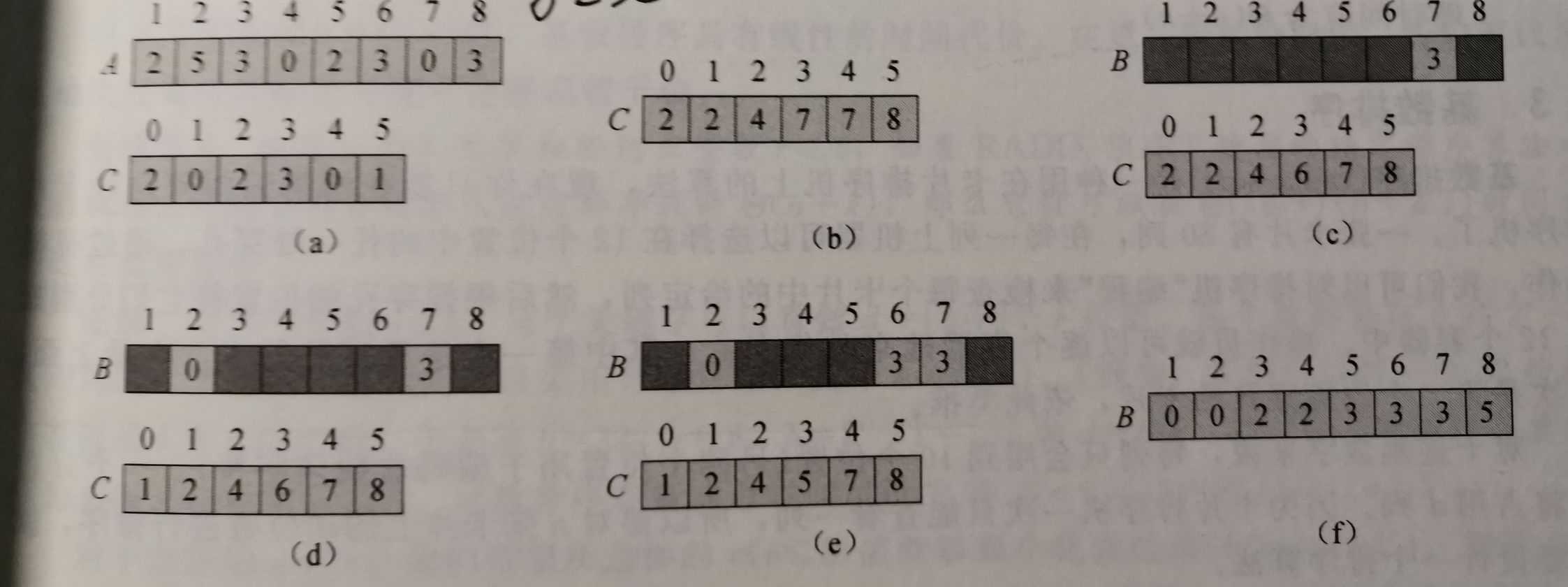
def Counting_Sort(A,B,k):
    for i in range(k+1):
        c[i]=0
    for j in range(1,len(A)):
        c[A[j]]=c[A[j]]+1
    for i in range(1,k+1):
        c[i]=c[i]+c[i-1]
    for j in range(len(A),0,-1):
        B[c[A[j]]]=A[j]
        c[A[j]]=c[A[j]]-1

　　 排序代价为theta(n)。同时上述算法是稳定的，也就是说对于两个相同的数来说，在输入数组中先出现的数，在输出数组中也位于前面。

　　实际上是因为我们在最后的给B赋值过程中，用的倒叙。

 

基数排序：

　　基数牌组法先是按最低有效位进行排序。为确保基数排序的正确性，一位排序算法必须是稳定的。

#include <iostream>
#include <time.h>
using namespace std;
const n=10,m=4;
int Max(int B[n][m],int h)//O(n)
{//求最大k值
    int k=0;
    for (int i=0;i<n;i++)//O(n)
    {
        if (B[i][h]>k)
        {
           k=B[i][h];
        }
    }
    return k;
}
void COUNTING_SORT(int B[n][m],int C[n],int k,int h)//O(k)+O(n)+O(k)+O(n)=O(n+k)
{//计数排序
   
    int *D=new int[k+1];
    for (int i=0;i<=k;i++)//O(k)
    {
        D[i]=0;
    }
    for (int j=0;j<n;j++)//O(n)
    {
        D[B[j][h]]=D[B[j][h]]+1;
    }
    for (i=0;i<=k;i++)//O(k)
    {
        D[i+1]=D[i+1]+D[i];
    }
    for (j=n-1;j>=0;j--)//O(n)
    {
        C[D[B[j][h]]-1]=j;//把排好序的下标存放到数组C中以便按顺序把它存储到辅助数组E中。
        D[B[j][h]]=D[B[j][h]]-1;
    }
}
int Converted_to_Decimal(int A[],int B[][m],int i)//O(d)+O(d)=O(d)
{//此函数是将十进制数以2维数组B的形式存放。
    int x=A[i];
    for (int j=0;x>0;j++ )//O(d)循环了j<d次
    {
        B[i][j]=x%10;
        x=x/10;
    }
    if (j<m)
    {
        for (int k=j;k<m;k++)//O(d) 循环了d-j次
        {
            B[i][k]=0;
        }
    }
    return j;
}
void Radix_sort(int A[n],int B[][m],int C[n],int E[n],int d)
{
    d=m;
    for ( int i=0;i<n;i++)//O(nd)
    {
        Converted_to_Decimal(A,B,i);
    }
    for ( i=0;i<d;i++)//O(d) d为位数
    {//因为d<=d位数的最小值<=k,(例如3<3位数最小值100)所以d<=n+k,内层循环O(n)+O(n+k)+O(n)+O(n)+O(d)+O(n)=O(n+k)
        int k=Max(B,i);//O(n)
        COUNTING_SORT(B,C,k,i);//O(n+k)
        for (int i=0;i<n;i++)//O(n)
        {
            E[i]=A[C[i]];//每位上排好序后，将其复制到辅助数组E上。
        }
        for ( i=0;i<n;i++)//O(n)
        {
            Converted_to_Decimal(E,B,i);//把辅助数组E上的数转换成二维数组存放到二维数组B中。
        }
        for (i=0;i<n;i++)//O(n)
        {
            A[i]=E[i];//每次将按位排好序的数存放到数组A中以便在下一次循环中对下一位进行排序。
        }
    }//所以Radix_sort时间复杂度为O(d(n+k))
    //O(nd)+O(d(n+k))=O(d(n+k))
}
void main()
{
    srand( (unsigned)time( NULL ) );
    int A[n]={0};
    for (int i=0;i<n;i++)
    {
        A[i]=rand()%(n);
    }
    int  B[n][m]={0},C[n]={0},E[n]={0};
    Radix_sort(A,B,C,E,m);
    for ( i=0;i<n;i++)
    {
        cout<<A[i]<<" ";
    }
}

　　更加详细，请看：https://blog.csdn.net/z84616995z/article/details/18502085

 

桶排序法：

　　桶排序法假设了输入数据服从均匀分布，平均情况下时间代价为theta(n)。桶排序将[0, 1)区间分为n个相同大小额子区间，称之为桶。然后，将n个输入书分别放到各个同中。这里，我们按找顺序放进桶，桶中的元素是无序的。

class bucketSort(object):
    def insertSort(self,a):
        n=len(a)
        if n<=1:
            pass
        for i in range(1,n):
            key=a[i]
            j=i-1
            while key<a[j] and j>=0:
                a[j+1]=a[j]
                j-=1
            a[j+1]=key
    def sort(self,a):
        n=len(a)
        s=[[] for i in xrange(n)]
        for i in a:
            s[int(i*n)].append(i)
        for i in s:
            self.insertSort(i)
        return [i for j in s for i in j]
    def __call__(self,a):
        return self.sort(a)