DFS序

Posted 2021-02-28 sweetlittlebaby

dfs序就是一棵树在dfs遍历时组成的节点序列.（先序遍历差不多），dfs序把一棵树进行区间化

出入的区间就是它掌控的子树，出入分别即为in[x],out[x],in[x]为结点x进入时的时间戳，out[x]为结点x出去时的时间戳

 

 

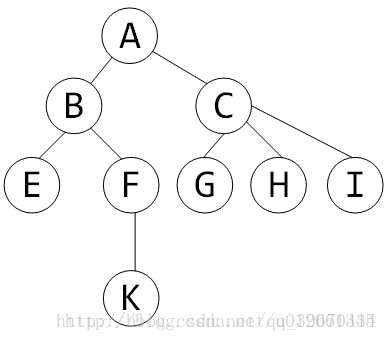
 比如上图子树，dfs序为，A B E E F K K F B C G G H H I I C A; （插入，括号化定理）

对于一棵树的dfs序而言，同一棵子树所对应的一定是dfs序中连续的一段。

在正常dfs数组下用辅助数组记录一下dfs序即可；

in[x]表示映射的DFS预处理出的线性结构，也就是说x是原始节点，in[x]是x节点的新位置，num[tot]表示第tot个节点的编号，num[in[x]]表示的还是x。num是新序列，in表示是新序列的下标，in[x]~out[x]是x为根结点的子树，划分为一个区间。 

基础代码：

int tot=0;
inline void dfs(int x,int fa)
{
    in[x]=++tot;
    num[tot]=x;//生成新的线性结构
    for(int i=0; i<G[x].size(); i++)
    {
        int cnt=G[x][i];
        if(cnt==fa) continue;
        dfs(cnt,x);
    }
    out[x]=tot;
}

给定一棵树，和每个结点的权值，则有以下关于dfs序的问题：

1，单点修改，子树和查询；

简单来说就给一个节点加上权值w，查询一颗子树的总和（废话）

每个子树在dfs序中都是一段连续的区间，然后维护一个dfs序，树状数组实现，单点修改，区间查询；

2，树链修改，单点查询；

给从u->v的链上的每个权点+W，查询某个节点的权值；

显然直接操作比较困难，那就间接操作；

a，对x到根节点路径上所有点权加W，

b，对Y到根节点路径上所有点权加W

c. 对LCA(x, y)到根节点路径上所有点权值减W（LCA（Least Common Ancestors）最近公共祖先）

d. 对LCA(x,y)的父节点 fa(LCA(x, y))到根节点路径上所有权值减W

要进行四次这样从一个点到根节点的区间修改.；

进行一个点X到根节点的区间修改, 查询其他一点Y时,只有X在Y的子树内, X对Y的值才有贡献且贡献值为W.

当单点更新X时,X实现了对X到根的路径上所有点贡献了W.于是只需要更新四个点(单点更新) ,查询一个点的子树内所有点权的和(区间求和)即可.

这样就会实现点修改，区间查询；（用树状数组和线段树都可）

3，树链修改，子树和查询；

修改同2，子树和查询；

方法也同二，问题转化为修改某个点到根节点的距离；

当修改某个节点A, 查询另一节点B时

只有A在B的子树内, Y的值会增加

W * (dep[A] - dep[B] + 1) => W * (dep [A] + 1) - W * dep[B]

所以用两个树状数组或线段树即可：

处理出数组Sum1,每次更新W*(dep[A]+1),和数组Sum2,每次更新W.

每次查询结果为Sum1(R[B]) – Sum1(L[B]-1) - (Sum2(R[B]) – Sum2(L[B]-1)) * dep [B].

有时间再写（逃......