数据结构——STL栈与后缀表达式

Posted 2021-02-28 zaza-zt

Part 1：栈是什么

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。

这一端被称为栈顶，相对地，把另一端称为栈底。

向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；

从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

——来自百度百科

那么栈通俗来讲是什么意思呢？

大家可以想象一下餐厅清洁工。

假如笔者是一个可怜的洗碗工，当顾客吃完饭的时候，盘子总是堆成一堆，摆在我面前。

我每次只能拿最上面的那个盘子清洗。（拿最下面的会倒塌打碎盘子）

比如有三个盘子，我每分钟可以清洗一个盘子，当我清洗完第二个的时候，很不幸，又来了三个盘子。

所以我只能先清洗第二次来的那三个盘子。具体模拟情况如下。

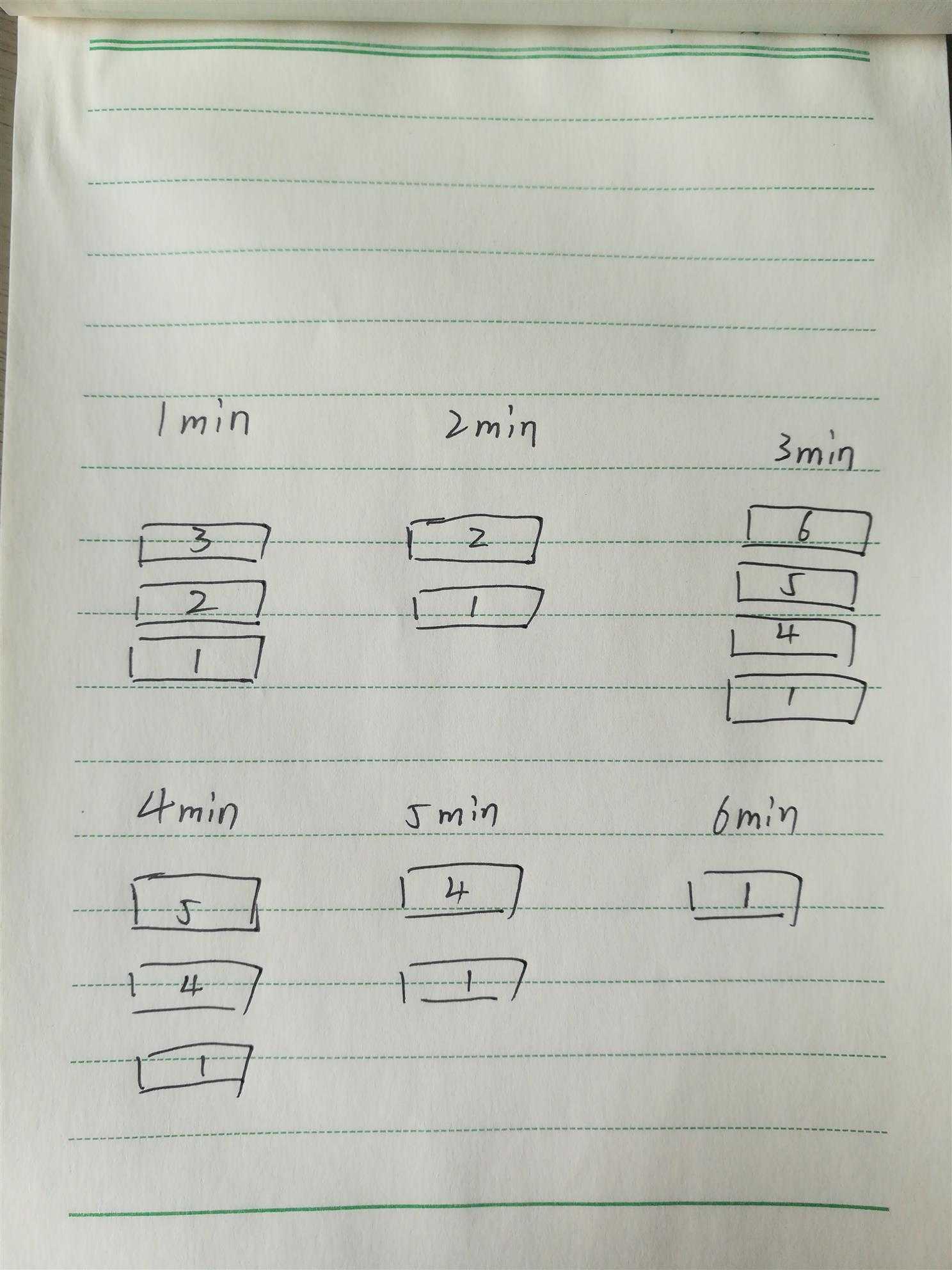
结合图片（我手画的很丑），我们不难看出，当第一次给我三个盘子的时候，第一个盘子在最下面。

最后给我的3号盘子被优先清洗，第二次给我3个盘子的时候，最先进入的4号盘子在最下面，最后进入的6号盘子在最上面，也是最先清洗的。

这就是“栈(stack)”——一种先进后出的数据结构。

Part 2：栈能做什么？

很多，比如后缀表达式求值，或者自动监测括号匹配等等。今天的例题就是后缀表达式求值问题。

Part 3：如何模拟栈？

如果您是dalao，可以用各种指针手写栈，但是如果嫌麻烦的话，STL库里有与栈相关的函数和数据结构。

#include<stack>

这是STL栈的头文件，包含以下函数。

首先声明栈，声明方式为stack<数据类型>名字;

比如stack<int>s;

s.empty()       如果栈为空返回true，否则返回false
s.size()        返回栈中元素的个数
s.pop()        删除栈顶元素
s.top()       指向栈顶的元素的指针
s.push()        在栈顶压入新元素

使用方式也和STL队列大同小异。

Part 4：例题，后缀表达式

相信大家在这时已经大概理解了什么是栈，以及栈的使用方法，上一个简单的例题

洛谷P1449 后缀表达式

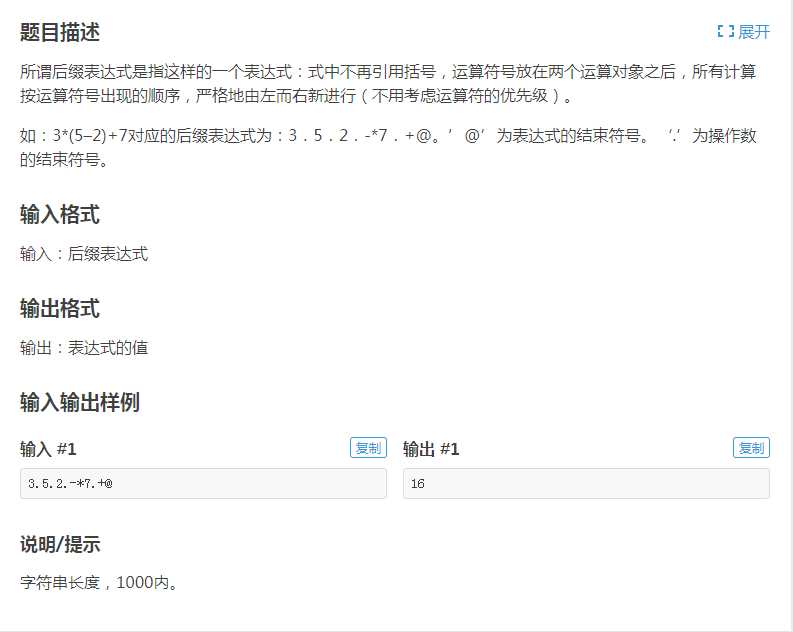
首先我们说说后缀表达式到底是个什么东西。

题目中已经给了描述，大概意思就是只要遇到了任何一个运算符号，我们就把之前的两个数用这个运算符运算变成一个数，然后继续向后进行。

我这里提供一种思路（仅供参考，dalao们请自觉退出，避免窥探蒟蒻的世界）

我们可以维护一个栈。

我们按顺序检索表达式，把数字入栈，当检索到一个运算符的时候，就把之前进入栈的两个数拿出来运算，然后把运算后的新数再次入栈

如此进行直到表达式结束。

问题又来了，怎么把数字由字符类型变成int类型来计算呢？

这里我用了更加蒟蒻的方法，队列+乘方。

请dalao们康康伪代码。

char read[5010];
int len2=-1,x;//注意是-1，如果是0会导致数字变成原来的10倍 
queue<int>q;
stack<int>stk; 
if(‘0‘<=read[i]&&read[i]<=‘9‘)
{
    mmp=read[i]-‘0‘;//当检测到的字符是一个数字的时候，把他转化为int类型的数字 
    q.push(mmp);//进入队列 
    len2++;//数字长度(位数)++ 
}
if(read[i]==‘.‘)//当检测到"."的时候，说明这个数字已经读完了 
{
    while(q.size()!=0)//当队列不为空的时候，执行以下操作 
    {
        x+=q.front()*pow(10,len2);//用队列的第一个元素乘以10的len2次方，然后累加 
        q.pop();//弹出队首 
        len2--;//长度-- 
    }
    stk.push(x);//检测完这个数字，把它压栈 
    x=0;//清零变量，准备下一次读入 
}

这是我把字符数转化为int数的方法，代码注释已经很详细了，这里不多BB

（欢迎大佬提出更好的想法狙击我）

既然数据类型转化做完了，下面的工作就明朗起来了，只要读入运算符，就弹出栈的前两个元素，然后执行运算操作，把新数压入栈顶就OK了

下面是本蒟蒻的完整AC代码：

//P1449
//#include<zhangtao.std>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<stack>
#include<queue>
#include<cmath>//一堆头文件，遵循“就算饿死，从这里跳下去，也不开万能头”的原则  
using namespace std;
char read[1010];
int len1,mmp,len2=-1,x,a,b;
stack<int>stk;
queue<int>q;
int main()
{
    scanf("%s",read);//读入字符串，超级香的scanf 
    len1=strlen(read);//统计字符数组长度 
    for(int i=0;i<len1;i++)//检索整个字符数组 
    {
        if(‘0‘<=read[i]&&read[i]<=‘9‘)
        {
            mmp=read[i]-‘0‘;
            q.push(mmp);
            len2++;
        }
        if(read[i]==‘.‘)
        {
            while(q.size()!=0)
            {
                x+=q.front()*pow(10,len2);
                q.pop();
                len2--;
            }
            stk.push(x);
            x=0;
        }//上面的刚才已经提到过 
        if(read[i]==‘-‘)
        {
            a=stk.top();//存下第一个元素 
            stk.pop();//弹出 
            b=stk.top();//存下第二个元素 
            stk.pop();//弹出 
            stk.push(b-a);//执行减法操作，把结果入栈
        }
        if(read[i]==‘+‘)
        {
            a=stk.top();
            stk.pop();
            b=stk.top();
            stk.pop();
            stk.push(b+a);
        }//同上 
        if(read[i]==‘*‘)
        {
            a=stk.top();
            stk.pop();
            b=stk.top();
            stk.pop();
            stk.push(b*a);
        }//同上 
        if(read[i]==‘/‘)
        {
            a=stk.top();
            stk.pop();
            b=stk.top();
            stk.pop();
            stk.push(b/a);
        }//本题的数据可以直接除(满足C++int类型除法的运算原则) 
    }
    cout<<stk.top();//输出最后一个元素(即为结果) 
    return 0; 
}

好了今天的分享（水博）就到这里，同学们下次再见！（下次可能又一个月之后了）