n皇后问题 非递归解法1

Posted 2021-02-28 realize1536799

运行结果：

 

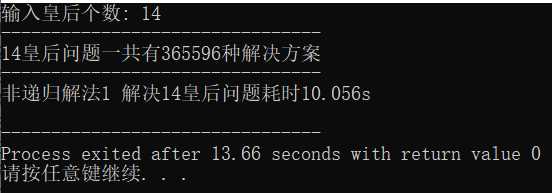
代码如下：

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 #include <bits/stdc++.h>
 4 using namespace std;
 5 const int MAX = 1024;
 6 const char *LINE32 = "--------------------------------";
 7 const bool PRINT_DETAILS = false; 
 8 long long n, cnt = 0;    // n表示皇后数量，cnt表示方案数量 
 9 int queen[MAX+1];
10 
11 void print() {
12     cout << LINE32 << endl;
13     cout << "第" << cnt << "个解法: " << endl;
14     for (int i = 1; i <= n; i++) {
15         if (i != 1) {
16             cout << ", ";
17         }
18         cout << "(" << i << "," << queen[i] << ")";
19     } 
20     cout << endl;
21     for (int i = 1; i <= n; i++) {
22         for (int j = 1; j <= n; j++) {
23             if (queen[i] != j) {
24                 cout << ‘x‘;
25             } else {
26                 cout << ‘Q‘;
27             }
28         }
29         cout << endl;
30     }
31 }
32 
33 bool check(int row, int col) {    // 检查是否可以在（row，col）这个坐标放置皇后 
34     for (int placed = 1; placed < row; placed++) {
35         if (queen[placed]==col || abs(row-placed)==abs(col-queen[placed])) {
36             return false;
37         }
38     }
39     return true;
40 }
41 void solve(int n) {
42     int row = 1;    // row表示当前正在放置的行，初始值为1，表示从第一行开始放置皇后
43     queen[row] = 1;        // 即a[1]=1，表示初始时，先放一个皇后在（1，1）
44     while (row > 0) {    // row的值最后为0，因为所有情况都检查完时，第一行往上回溯，row值就为0
45         if (row > n) {
46             // 找到一个解，之后需要向上回溯：从上一行的下一列开始检查 
47             cnt++;
48             if (PRINT_DETAILS) {
49                 print();
50             } 
51             queen[--row]++; 
52         } else if (queen[row] > n) {
53             // queen[row]表示的是当前row行上待检测的列的位置 
54             // 此时row行已经全部的位置都检查完了，同样的向上回溯：从上一行的下一列开始检查 
55             queen[--row]++; 
56         } else if (check(row, queen[row])) {
57             // 找到一个符合的位置，开始放置下一行，从第一列开始 
58             queen[++row] = 1; 
59         } else {
60             // 此时表示这个位置不符合，查看这一行下一列的位置
61             queen[row]++; 
62         } 
63     } 
64 } 
65 
66 int main() {
67     // input
68     cout << "输入皇后个数: "; 
69     cin >> n;
70     // compute
71     clock_t begin = clock(); 
72     solve(n); 
73     clock_t end = clock(); 
74     // output
75     cout << LINE32 << endl;
76     cout << n << "皇后问题一共有" << cnt << "种解决方案" << endl; 
77     cout << LINE32 << endl;
78     cout << "非递归解法1 解决" << n << "皇后问题耗时" << /*end-begin << "打点" <<*/(double)(end-begin)/CLOCKS_PER_SEC  << "s" << endl;
79     return 0;
80 } 
81 // 14 9~11s

 

与递归解法1对比：

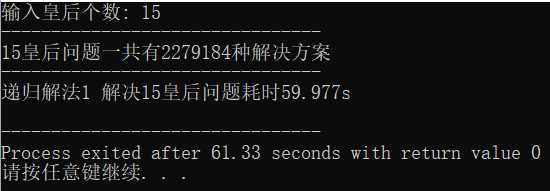
①递归解法1运行情况：

②非递归解法1运行情况：

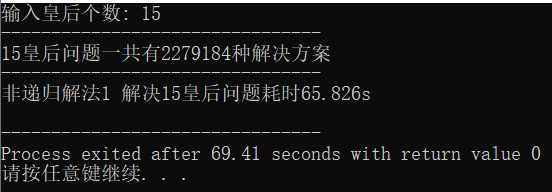
可以看到，非递归解法1比递归解法1运行时间略多一些，这不符合预期，按理来说，非递归解法运行时间应该更短，下一篇博客将对比非递归解法2与递归解法2。