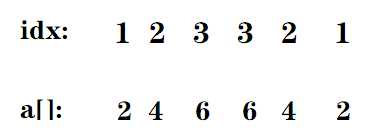CF58C Trees(逆向思维)

Posted 2021-02-28 liyexin

地址：https://www.baidu.com/link?url=fJ5P3mDdJxPJPBMMaMXI6rddzPrI892EBzpxZQlF6sTvD1CnfcXu-4xpjLYvfolK&wd=&eqid=87db10e900010a0b000000045e9da0fc

题目描述

On Bertown‘s main street nn trees are growing, the tree number ii has the height of a_{i}ai? meters ( 1<=i<=n1<=i<=n ). By the arrival of the President of Berland these trees were decided to be changed so that their heights formed a beautiful sequence. This means that the heights of trees on ends (the 11 st one and the nn -th one) should be equal to each other, the heights of the 22 -nd and the (n-1)(n−1) -th tree must also be equal to each other, at that the height of the 22 -nd tree should be larger than the height of the first tree by 11 , and so on. In other words, the heights of the trees, standing at equal distance from the edge (of one end of the sequence) must be equal to each other, and with the increasing of the distance from the edge by 11 the tree height must also increase by 11 . For example, the sequences "2 3 4 5 5 4 3 2" and "1 2 3 2 1" are beautiful, and ‘1 3 3 1" and "1 2 3 1" are not.

Changing the height of a tree is a very expensive operation, using advanced technologies invented by Berland scientists. In one operation you can choose any tree and change its height to any number, either increase or decrease. Note that even after the change the height should remain a positive integer, i. e, it can‘t be less than or equal to zero. Identify the smallest number of changes of the trees‘ height needed for the sequence of their heights to become beautiful.

输入格式

The first line contains integer nn ( 1<=n<=10^{5}1<=n<=105 ) which is the number of trees. The second line contains integers a_{i}ai? ( 1<=a_{i}<=10^{5}1<=ai?<=105 ) which are the heights of the trees.

输出格式

Print a single number which is the minimal number of trees whose heights will have to be changed for the sequence to become beautiful.

Examples

Input

3
2 2 2

Output

1

Input

4
1 2 2 1

Output

0

　　　　题意：美丽序列：回文，左边一半是连续递增，增加值都一样，右边和左边一一对应。操作是选取一个数，改成任意值。要想把给出的序列变成美丽序列，求最少改动的数的数量。
　　　　解析：想了一下，要想求最少改动次数，的确不容易。逆向思维一下，最少改动次数=n-最多不需要改动数。对于序列 2 4 6 6 4 2，有：
　　　　　 

 　　　　　　　 可以看出，美丽序列的每一个a[]-idx都相等(idx也要对称)，而且a[]-idx>=0。既然都相等，所以我们统计一下每个差值出现的次数，出现最多的，就不需要改动，n-maxx就是最少改动次数了

#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
using namespace std;
const int maxn=1e5+10;
int a[maxn];
int main()
{
    int n;
    cin>>n;
    map<int,int>mp;
    int maxx=0;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
        int md=a[i]-min(i,n-i-1);
        if(md>=0)
        {
            mp[md]++;
            maxx=max(maxx,mp[md]);
        }
    }
    cout<<n-maxx<<endl;
}