选第k小元素：特定分治策略

Posted 2021-02-27 powerkeke

1. 问题

　　选出数组中第k小元素，采用分治算法。

 

2. 解析

分：将整个数组分为若干相等的块，各个块排序后找到其中位数。再将各个块的中位数集合，形成一个新数组，再次分块，不断分治后得到最终的中位数m。

治：找到m后，将原数组划分为3个组A1,A2,A3，分别包含小于，等于，大于m的元素。这样可以得到3中情况：

1. 若A1的元素数量大于等于K，即第K个元素在第一组内：在A1中递归查找第k小元素。
2. 若A1、A2元素个数之和大于等于K，即中项m为第K个元素。返回m。
3. 第K个元素在第三组：在A3中递归寻找第（k-|A1、A2元素数量之和|）小元素。

3. 设计

 n ← high - low + 1----（Θ(1)）  
if  n < 44 then 将 A 排序 return (A[k])----（Θ(1)）  
令 q =  ⌊n/5⌋。将 A 分成 q 组，每组5个元素。如果5不整除 n ，则排除剩余的元素。----（Θ(n)）  
将 q 组中的每一组单独排序，找出中项。所有中项的集合为 M。----（Θ(n)）  
mm ← select(M, 1, q,  ⌈q/2⌉)   { mm 为中项集合的中项 } ----T(n/5)  
将 A[low...high] 分成三组----（Θ(n)）  
    A1 = { a | a < mm }  
    A2 = { a | a = mm }  
    A3 = { a | a > mm }  
 case  
    |A1| ≥ k : return select(A1, 1, |A1|, k)  
    |A1| + |A2| ≥ k : return mm  
    |A1| + |A2| < k : return select(A3, 1, |A3|, k - |A1| - |A2|)  
end case  

 

4. 分析

上图中我们可以看到W区的元素都是小于或等于mm的，令A1’表示小于或等于mm的元素的集合，显然W会是A1’的子集，即A1’的元素数量大于等于W的元素数量。

于是我们有下面这个式子：

 　　

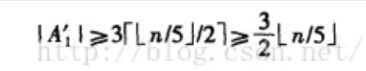
由对称性：

 　　

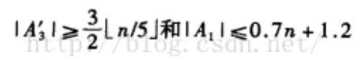
即：

 　　

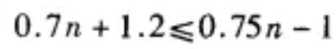
解不等式可得n>=44。

现在我们还有了算法运行时间的递推式：

可以算出来T(n)=Θ(n)。

对于求中项的题目也是同样的解法，就是找第（n+1）/2个元素（奇数）和第n/2、n/2+1个元素（偶数）。

 

 

5. 源码

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 7
void getData(int [], int);
void result_output(int []);
int selectmink1(int a[], int low, int high, int k);
int selectmink2(int a[], int low, int high, int k);
int split(int a[], int low, int high);
int main() {
    int a[N], k, r;

    getData(a, N); /* 获得数据放入数组a中 */

    printf("datas: 
");
    result_output(a);

    scanf("%d", &k);
    --k;
    if(k >= 0 && k <= N-1) {
        r = selectmink1(a, 0, N - 1, k);
        printf("result=%d
", r);
        r = selectmink2(a, 0, N - 1, k);
        printf("result=%d
", r);
    } else
        printf("input error: k=%d
", k);
    return 0;
}

int selectmink1(int a[], int low, int high, int k) {
    int middle;

    middle = split(a, low, high);
    if(middle == k)
        return a[k];
    else if(middle < k)
        return selectmink1(a, middle+1, high, k);
    else /* if(middle > k) */
        return selectmink1(a, low, middle-1, k);
}

int selectmink2(int a[], int low, int high, int k) {
    int middle;

    for(;;) {
        middle = split(a, low, high);
        if(middle == k)
            return a[k];
        else if(middle < k)
            low = middle+1;
        else /* if(middle > k) */
            high = middle-1;
    }
}

int split(int a[], int low, int high) {
    int part_element = a[low];

    for (;;) {
        while (low < high && part_element <= a[high])
            high--;
        if (low >= high) break;
        a[low++] = a[high];

        while (low < high && a[low] <= part_element)
            low++;
        if (low >= high) break;
        a[high--] = a[low];
    }

    a[high] = part_element;
    return high;
}

void getData(int d[], int n) {
    time_t t;
    srand((unsigned) time(&t));  /* 设置随机数起始值 */

    int i;
    for(i=0; i < n; i++)
        d[i] = rand() % 100; /* 获得0-99之间的整数值 */
}

void result_output(int a[]) {
    int i;
    for (i = 0; i < N; i++)
        printf("%d ", a[i]);
    printf("
");
}

 

参考：https://www.jianshu.com/p/2759d3c21bd9