凸多边形的划分 LibreOJ - 10149

Posted 2021-02-27 xxxsans

给定一个具有 NN 个顶点的凸多边形，将顶点从 11 至 NN 标号，每个顶点的权值都是一个正整数。将这个凸多边形划分成 N−2N−2 个互不相交的三角形，试求这些三角形顶点的权值乘积和至少为多少。

Input

输入第一行为顶点数 NN

第二行依次为顶点 11 至顶点 NN 的权值。

Output

输出仅一行，为这些三角形顶点的权值乘积和的最小值。

Example

样例输入

5
121 122 123 245 231

样例输出

12214884

Hint

对于 100%100% 的数据，有 N≤50N≤50，每个点权值小于 109109。

 

思路

首先随便搞一个多边形：

然后给它顺时针每个顶点表上序号：

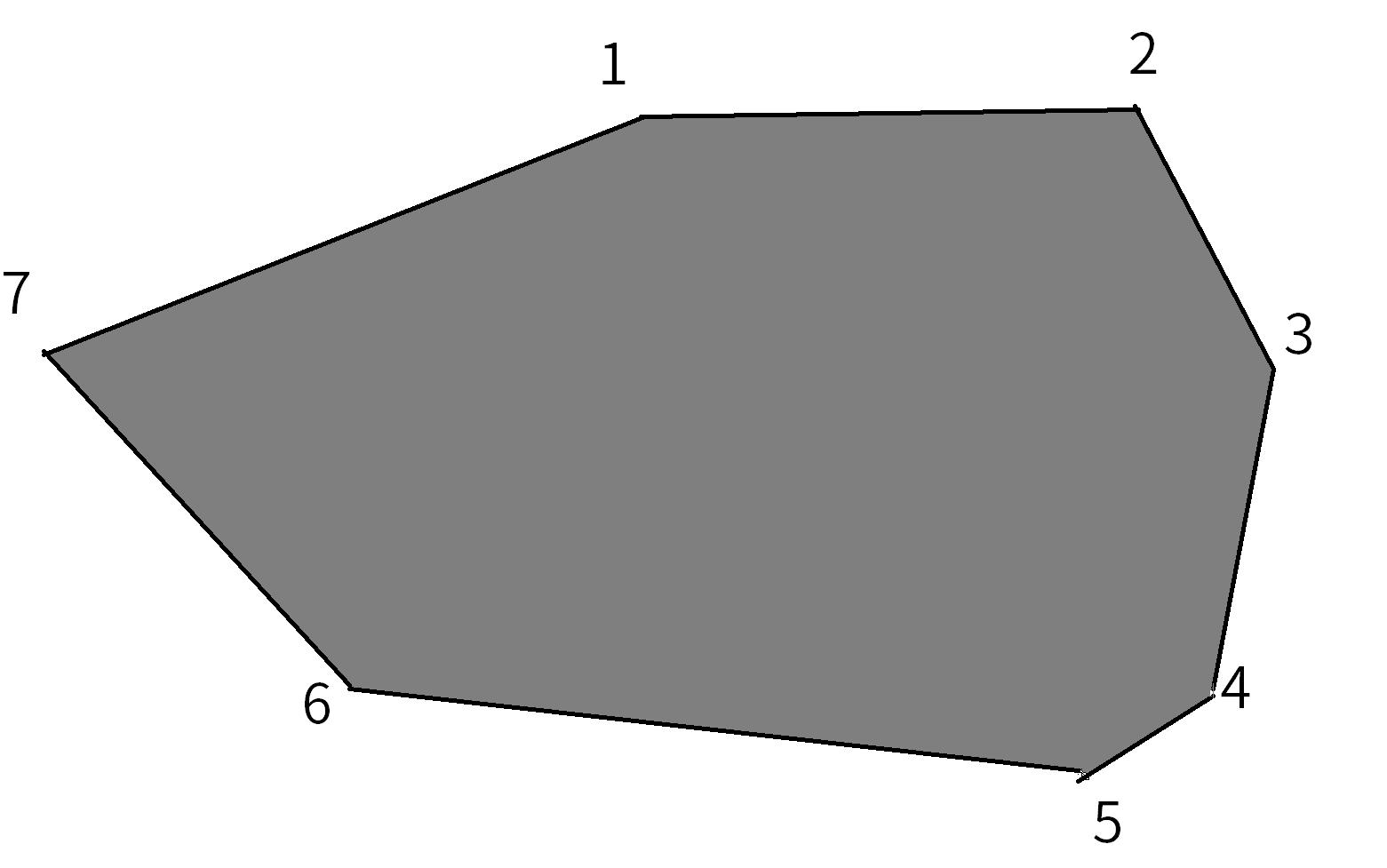
然后枚举i,ji,j，要求：i+1<ji+1<j，然后给i,ji,j连一条线，分割出来另一个多边形：多边形23456

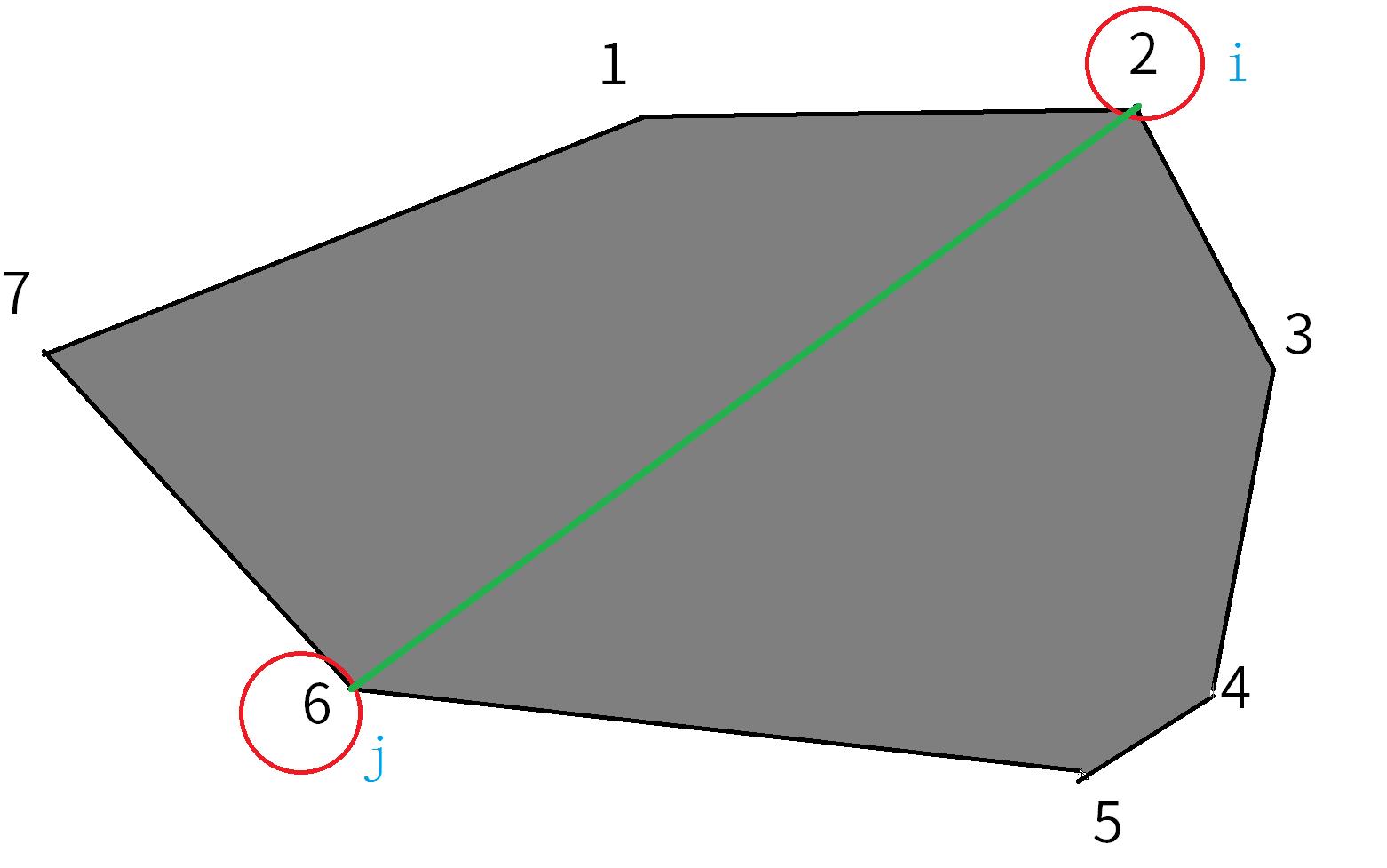
然后在i,ji,j范围内枚举kk，使得多边形23456又可以分割。

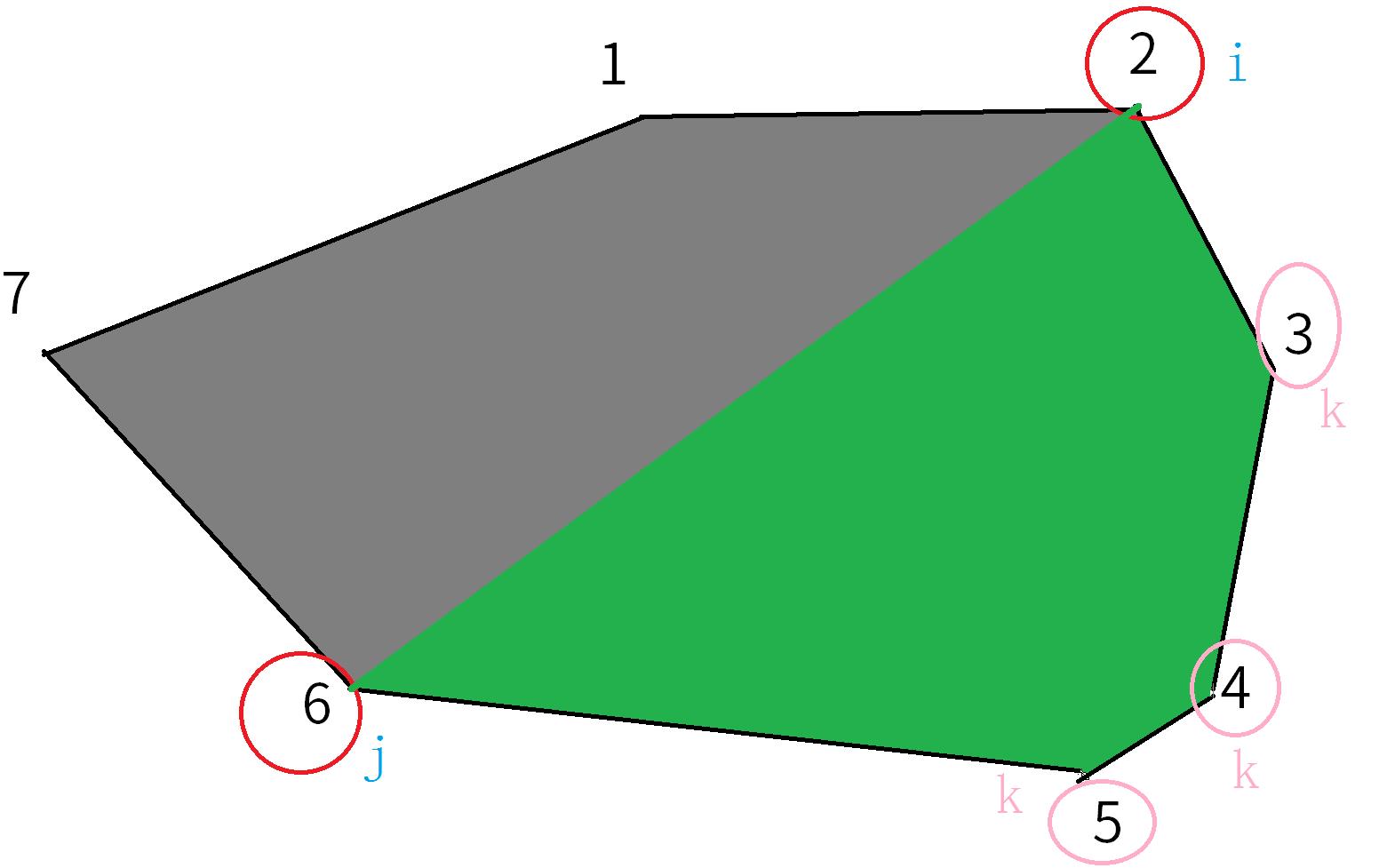
分割成如下图：

设f[i][j]f[i][j]表示把i,ji,j的多边形切割成三角形后的权值乘积之和的最小值。

可得：

 

f[i][j]=min{f[i][k]+f[k][j]+a[i]∗a[j]∗a[k]}(0<i<j<k≤n)f[i][j]=min{f[i][k]+f[k][j]+a[i]∗a[j]∗a[k]}(0<i<j<k≤n)

 

初始化：

 

f[i][j]=inf(0<i≤n,0<j≤n)f[i][j]=inf(0<i≤n,0<j≤n)

 

f[i][i+1]=0(0<i<n)f[i][i+1]=0(0<i<n)

 

时间复杂度：O(n3)O(n3)

输出结果：f[1][n]f[1][n]

当然，这道题范围特别大：对于 100100 的数据，有 N≤50N≤50，每个点权值小于 109109。三个数相乘最高可达10271027，所以需要使用高精度。这里使用了C++大数类，转自代号4101

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000;  
struct bign{  
    int d[maxn], len;  
  
    void clean() { while(len > 1 && !d[len-1]) len--; }  
  
    bign()          { memset(d, 0, sizeof(d)); len = 1; }  
    bign(int num)   { *this = num; }   
    bign(char* num) { *this = num; }  
    bign operator = (const char* num){  
        memset(d, 0, sizeof(d)); len = strlen(num);  
        for(int i = 0; i < len; i++) d[i] = num[len-1-i] - ‘0‘;  
        clean();  
        return *this;  
    }  
    bign operator = (int num){  
        char s[20]; sprintf(s, "%d", num);  
        *this = s;  
        return *this;  
    }  
  
    bign operator + (const bign& b){  
        bign c = *this; int i;  
        for (i = 0; i < b.len; i++){  
            c.d[i] += b.d[i];  
            if (c.d[i] > 9) c.d[i]%=10, c.d[i+1]++;  
        }  
        while (c.d[i] > 9) c.d[i++]%=10, c.d[i]++;  
        c.len = max(len, b.len);  
        if (c.d[i] && c.len <= i) c.len = i+1;  
        return c;  
    }  
    bign operator - (const bign& b){  
        bign c = *this; int i;  
        for (i = 0; i < b.len; i++){  
            c.d[i] -= b.d[i];  
            if (c.d[i] < 0) c.d[i]+=10, c.d[i+1]--;  
        }  
        while (c.d[i] < 0) c.d[i++]+=10, c.d[i]--;  
        c.clean();  
        return c;  
    }  
    bign operator * (const bign& b)const{  
        int i, j; bign c; c.len = len + b.len;   
        for(j = 0; j < b.len; j++) for(i = 0; i < len; i++)   
            c.d[i+j] += d[i] * b.d[j];  
        for(i = 0; i < c.len-1; i++)  
            c.d[i+1] += c.d[i]/10, c.d[i] %= 10;  
        c.clean();  
        return c;  
    }  
    bign operator / (const bign& b){  
        int i, j;  
        bign c = *this, a = 0;  
        for (i = len - 1; i >= 0; i--)  
        {  
            a = a*10 + d[i];  
            for (j = 0; j < 10; j++) if (a < b*(j+1)) break;  
            c.d[i] = j;  
            a = a - b*j;  
        }  
        c.clean();  
        return c;  
    }  
    bign operator % (const bign& b){  
        int i, j;  
        bign a = 0;  
        for (i = len - 1; i >= 0; i--)  
        {  
            a = a*10 + d[i];  
            for (j = 0; j < 10; j++) if (a < b*(j+1)) break;  
            a = a - b*j;  
        }  
        return a;  
    }  
    bign operator += (const bign& b){  
        *this = *this + b;  
        return *this;  
    }  
  
    bool operator <(const bign& b) const{  
        if(len != b.len) return len < b.len;  
        for(int i = len-1; i >= 0; i--)  
            if(d[i] != b.d[i]) return d[i] < b.d[i];  
        return false;  
    }  
    bool operator >(const bign& b) const{return b < *this;}  
    bool operator<=(const bign& b) const{return !(b < *this);}  
    bool operator>=(const bign& b) const{return !(*this < b);}  
    bool operator!=(const bign& b) const{return b < *this || *this < b;}  
    bool operator==(const bign& b) const{return !(b < *this) && !(b > *this);}  
  
    string str() const{  
        char s[maxn]={};  
        for(int i = 0; i < len; i++) s[len-1-i] = d[i]+‘0‘;  
        return s;  
    }  
};  
istream& operator >> (istream& in, bign& x){  
    string s;  
    in >> s;  
    x = s.c_str();  
    return in;  
}  
ostream& operator << (ostream& out, const bign& x){  

    out << x.str();  
    return out;  
}
#define ll bign
ll f[55][55],a[55];
int n;
int main(){
    cin>>n;
    for(int i=1;i<=n;i+=1) cin>>a[i];
    memset(f,63,sizeof(f));
    for(int i=1;i<=n;i++) f[i][i+1]=0;
    for(int L=2;L<=n-1;L++){
        for(int i=1;i<=n-L;i++){
            int j=i+L;
            for(int k=i+1;k<=j-1;k++){
                f[i][j]=min(f[i][k]+f[k][j]+a[i]*a[j]*a[k],f[i][j]);
            }
        }
    }
    cout<<f[1][n];putchar(‘
‘);
    return 0;
}

转自https://www.cnblogs.com/yzx1798106406/p/10327145.html#10085