数值计算方法实验之按照按三弯矩方程及追赶法的三次样条插值 (MATLAB 代码)
Posted ynly
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数值计算方法实验之按照按三弯矩方程及追赶法的三次样条插值 (MATLAB 代码)相关的知识,希望对你有一定的参考价值。
一、实验目的
在已知f(x),x∈[a,b]的表达式,但函数值不便计算,或不知f(x),x∈[a,b]而又需要给出其在[a,b]上的值时,按插值原则f(xi)= yi(i= 0,1…….,n)求出简单函数P(x)(常是多项式),使其在插值基点xi,处成立P(xi)= yi(i=0,1,……,n),而在[a,b]上的其它点处成立f(x)≈P(x).
二、实验原理

三、实验程序

四、实验内容
求之f(x)=x4在[0,2]上按5个等距节点确定的Lagrange插值多项式.
五、实验程序
syms x
f(x)=x^4;
a=0;
b=2; %左右断点值
n=4; %节点数为n+1
h=(b-a)/n;%h为相邻节点间的间距
u=1/2;
v=1/2; %等距节点下u,v的值一直为1/2
d=zeros(n+1,1);
D=zeros(n+1,n+1);
S=cell(4,1);
d(1)=12/h*((f(a+h)-f(a))/h-subs(diff(f(x)),x,a));
d(n+1)=12/h*(subs(diff(f(x)),x,b)-(f(b)-f(b-h))/h);
D(n+1,n+1)=4;
for i=2:n
d(i)=12*((f(a+h*i)-f(a+h*(i-1)))/h-(f(a+h*(i-1))-f(a+h*(i-2))/h))/(2*h);
end
for j=1:n
D(j,j)=4;
D(j,j+1)=v;
D(j+1,j)=u;
end
M=linsolve(D,d);
for k=1:n
s1=M(k,1)*(a+h*k-x)^3/(6*h)+M(k+1,1)*(x-a-h*(k-1))/(6*h)+f(a+h*(k-1)-M(k,1)*h*h/6)*((a+h*k-x)^3/(6*h)+M(k+1,1)*(x-a-h*(k-1)))/h+(f(a+h*k)-M(k+1,1)*h*h/6)*(x-a-h*(k-1))/h;
s2=vpa(s1,4);
S{k,1}=char(s2);
end
五、运算结果
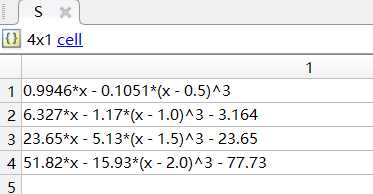
以上是关于数值计算方法实验之按照按三弯矩方程及追赶法的三次样条插值 (MATLAB 代码)的主要内容,如果未能解决你的问题,请参考以下文章