二分查找总结

Posted 2020-09-08

　　最近刷leetcode和lintcode，做到二分查找的部分，发现其实这种类型的题目很有规律，题目大致的分为以下几类：

　　1.最基础的二分查找题目，在一个有序的数组当中查找某个数，如果找到，则返回这个数在数组中的下标，如果没有找到就返回-1或者是它将会被按顺序插入的位置。这种题目继续进阶一下就是在有序数组中查找元素的上下限。继续做可以求两个区间的交集。

　　2.旋转数组问题，就是将一个有序数组进行旋转，然后在数组中查找某个值，其中分为数组中有重复元素和没有重复元素两种情况。

　　3.在杨氏矩阵中利用二分查找，针对矩阵性质的不同，有多种解法，可以对每一行遍历然后进行二分，也可以从左下角进行二分查找，也可以从右上角进行二分查找。

　　4.函数的极大值问题，就是在一个数组中求极大值，极大值就是某个数大于数组当中左右两边的数，位于端点的元素只需大于它挨着的元素就行。典型的例题就是寻找峰值问题。

　　5.利用极限和二分查找的思想，进行幂运算，开平方根和对数函数的求解，对于浮点数和整数有何异同。

二分查找的区间控制的三种方式：

　　1.闭区间

　　　　取值的范围是[left,right]，一定要保证每次循环结束后left+1或者right-1，结束的状态left>right,left在右边，right在左边，目标值下标确定是left。

　　2.开区间

　　　　取值范围是[left,right),right无法得到，它有两种形式left+1<right和left<right.

　　　　当是left+1<right这种形式时，left和right都不需要加一或者减一，结束状态是left<right，无法确定最后的目标值下标是left还是right，最后还需要做一次判断。

　　　　当是left<right这种形式时，left需要加一，结束状态是left>right,left在right右边，left的位置就是所求结果的位置。在集合中进行二分查找，比较nums[mid]，此时要与nums[right]进行比较。

1.基础二分查找，查找上下限，求两个区间的交集

　　 例如leetcode278题，题目如下：

 

You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.

Suppose you have n versions [1, 2, ..., n] and you want to find out the first bad one, which causes all the following ones to be bad.

You are given an API bool isBadVersion(version) which will return whether version is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.

 

　　这是一个典型的二分查找问题，题目的解如下：

　　整个二分查找分为控制区域和判断函数，控制区域是为了选择合适的值，判断函数用来判断值是否正确。控制区域的边界是特别容易出错的地方，一般有闭区间和开区间两种方式，我做题的时候一般用的是闭区间，假设存在low和high两个指针，那么闭区间的范围就是[low,high]，一定要保证每次循环结束后low+1或者high-1，结束状态是low>high，low在右边，high在左边，目标值的下标确定是left。

　　接着看另一个题目搜索插入位置http://www.lintcode.com/problem/search-insert-position如下：

 

给定一个排序的整数数组（升序）和一个要查找的整数target，用O(logn)的时间查找到target第一次出现的下标（从0开始），如果target不存在于数组中，返回-1。
样例

[1,3,5,6]，5 → 2

[1,3,5,6]，2 → 1

[1,3,5,6]， 7 → 4

[1,3,5,6]，0 → 0

 

这个题目是寻找在数组中的下标，如果没找到则返回它应该被查入的位置，代码如下：

 

public class Solution {
    /** 
     * param A : an integer sorted array
     * param target :  an integer to be inserted
     * return : an integer
     */
    public int searchInsert(int[] A, int target) {
        // write your code here
        if (A == null || A.length == 0) {
            return 0;
        }
        int low = 0;
        int high = A.length - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (A[mid] == target) {
                return mid;
            } else if (A[mid] > target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        low = 0;
        high = A.length - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (A[mid] < target) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        return low;
    }
}

 

另一类题目http://www.lintcode.com/zh-cn/problem/search-for-a-range/是寻找一个有序数组中元素的上下限，也可以是元素在数组中出现的下标范围，题目如下：

给定一个包含 n 个整数的排序数组，找出给定目标值 target 的起始和结束位置。

如果目标值不在数组中，则返回[-1, -1]

样例
给出[5, 7, 7, 8, 8, 10]和目标值target=8,

返回[3, 4]

先判断该元素是否在数组中，如果不在返回[-1,-1]，否则，先查找下限位置，在查找上限位置，查找下限时直接判断nums[mid]<target是否成立，是的话low=mid+1，查找上限时判断nums[mid]>target是否成立，如果成立high=mid-1,代码如下：

 

public class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] res = {-1, -1};
        if (nums == null || nums.length == 0) {
            return res;
        }
        int start = findLow(nums, target);
        int end = findHigh(nums, target);
        res[0] = start;
        res[1] = end;
        return res;
    }
    public int findLow(int[] nums, int target) {
        int idx = -1;
        int low = 0;
        int high = nums.length - 1;
        int mid;
        while (low <= high) {
            mid = low + ((high - low) >> 1);
            if (nums[mid] < target) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
            if (nums[mid] == target) idx = mid;
        }
        return idx;
    }
    public int findHigh(int[] nums, int target) {
        int idx = -1;
        int low = 0;
        int high = nums.length - 1;
        int mid;
        while (low <= high) {
            mid = low + ((high - low) >> 1);
            if (nums[mid] > target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
            if (nums[mid] == target) idx = mid;
        }
        return idx;
    }
}

 

 

 

还有另一种解法是先调用Arrays.binarySearch(nums,target)查找到target的位置，然后让start=mid，当start>=0&&nums[start]==target，start--，循环结束后在进行一次start++，对end也是如此，这样的时间复杂度也是Olog(n)，代码如下：

 

public class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] res = {-1, -1};
        if (nums == null || nums.length == 0) {
            return res;
        }
        int mid = binarySearch(nums, target);
        if (mid < 0) {
            return res;
        }
        int start = mid;
        while (start >= 0 && nums[start] == target) {
            start--;
        }
        start++;
        res[0] = start;
        int end = mid;
        while (end < nums.length && nums[end] == target) {
            end++;
        }
        end--;
        res[1] = end;
        return res;
    }
    
    public int binarySearch(int[] nums, int target) {
        int idx = -1;
        int low = 0;
        int high =nums.length - 1;
        int mid;
        while (low <= high) {
            mid = low + ((high - low) >> 1);
            if (nums[mid] == target) {
                idx = mid;
                break;
            } else if (nums[mid] > target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return idx;
    }
}

 

 

 

类似的题目有查找元素第一次出现的位置和最后一次出现的位置，如果找到，则返回元素位置，如果没找到，那么返回-1。例如以下例题，查找元素第一次出现的位置http://www.lintcode.com/zh-cn/problem/first-position-of-target/，题目如下：

 

给定一个排序的整数数组（升序）和一个要查找的整数target，用O(logn)的时间查找到target第一次出现的下标（从0开始），如果target不存在于数组中，返回-1。

样例
在数组 [1, 2, 3, 3, 4, 5, 10] 中二分查找3，返回2。

 

这道题其实相对简单，就是查找这个元素，找到的话直接返回位置，如果没有，则返回start的位置，需要注意的是，这道题在确定范围时判断条件不能是start<=end，需要是start<end，原因是当数组是[1,4,4,5,7,7,8,9,9,10]，当查找1时，如果是小于等于的话，那么最后由于查找到了，此时end=mid=start，这个时候就会进入死循环。具体的代码如下：

class Solution {
    /**
     * @param nums: The integer array.
     * @param target: Target to find.
     * @return: The first position of target. Position starts from 0.
     */
    public int binarySearch(int[] nums, int target) {
        //write your code here
        if (nums.length == 0 || nums == null) {
            return -1;
        }
        int start = 0;
        int end = nums.length - 1;
        while (start < end) {
            int mid = start + ((end - start) >> 1);
            if (nums[mid] == target) {
                end = mid;
            } else if (nums[mid] > target) {
                end = mid - 1;
            } else {
                start = mid + 1;
            }
        }
        if (nums[start] == target) {
            return start;
        }
        if (nums[end] == target) {
            return end;
        }
        return -1;
    }
}

里一个题就是查找元素最后出现的位置，题目如下：

给一个升序数组，找到target最后一次出现的位置，如果没出现过返回-1

样例

给出 [1, 2, 2, 4, 5, 5].

target = 2, 返回 2.

target = 5, 返回 5.

target = 6, 返回 -1.

如果这里的判断条件依然是start<end的话，代码就会进入死循环，因为在求mid的时候是向左边取整的。考虑这样的一个情况[...,5,5]，假设target为5，那么start就会一直向右靠近，最后到n-2的位置，而end此时为n-1，再次进入循环mid等于n-2，所以就进入了死循环。此时建议大家写成start + 1 < end，最后再判断start和end（按照所需先后判断）即可，这种写法适用于所有的情况，不容易出现问题。关键代码如下：

while (start + 1 < end) {
    int mid = (start + end)>>1;
    if (A[mid] > target) {
　　　　end = mid;
    } else { 
　　　　start = mid;
　　}
}

　　通过这两个题可以看出，在进行二分查找时，首先要缩小区间，然后剩下两个下标，最后再在判断两个下标，这样就把问题简化了。

另一种题目是求两个集合的交集，这种题目很简单，首先是对两个数组进行排序，然后遍历一个集合，把每一个数在另一个集合中进行二分查找，如果找到的话，就把该数加入到结果的集合中，时间复杂度是O(mlog(n))具体的代码如下：

 

    public ArrayList<Integer> FindElements(int[] nums1, int[] nums2) {
        if (nums1.length == 0 || nums2.length == 0 || nums1 == null || nums2 == null) {
            return null;
        }
        ArrayList<Integer> ans = new ArrayList<>();
        Arrays.sort(nums1);
        Arrays.sort(nums2);
        int key;
        for (int i = 0; i < nums1.length; i++) {
            key = nums1[i];
            int low = 0;
            int high = nums2.length - 1;
            while (low <= high) {
                int mid = low + ((high - low) >> 1);
                if (nums2[mid] == key) {
                    ans.add(key);
                    break;
                } else if (nums2[mid] < key) {
                    low = mid + 1;
                } else {
                    high = mid - 1;
                }
            }
        }
        return ans;
}

 

 

2.旋转数组问题

　　旋转数组就是将一个有序的数组，按照某个中轴进行前后旋转，例如[1,2,3,4,5,6]旋转后可能变为[3,4,5,6,1,2]，这种题目可以分为两种，在没有重复数字的旋转数组中查找某个元素，在有重复数字的数组中查找某个元素，首先看第一种：

　　这个题目解得时候，首先查找mid下标元素的值，判断nums[mid]是否等于target，如果是，返回1;如果不是的话就与low位置的值相比较，判断nums[low]<nums[mid]，如果是，那么这个范围内的数字是单调递增的，如果不是，那么这个范围内的数字不是单调的。如果是单调递增的，那么判断这个nums[low]<=target<=nums[mid]，是的话那么让high=mid，否则的话low=mid+1,；如果不是单调递增的话，那么判断nums[mid]=<target<=nums[high]，如果是的话，令low=mid,否则的话让high=mid-1。由于区间是low+1<high，所以最后要对结果进行验证，判断low和high哪一个符合要求，具体代码如下:

 

public class Solution {
    public int search(int[] nums, int target) {
        if (nums.length == 0 || nums == null) {
            return -1;
        }
        int low = 0;
        int high = nums.length - 1;
        while(low + 1 < high) {
            int mid = low + ((high - low) >> 1);
            if (nums[mid] == target) {
                return mid;
            }
            if (nums[mid] > nums[low]) {//前半部分是升序
                if (target >= nums[low] && target <= nums[mid]) {//待查找的元素再升序子序列中
                    high = mid;
                } else {
                    low = mid + 1;
                }
            } else if (nums[mid] < nums[low]){//前半部分不是升序
                if (target >= nums[mid] && target <= nums[high]) {
                    low = mid;
                } else {
                    high = mid - 1;
                }
            }
        }
        if (nums[low] == target) {
            return low;
        }
        if (nums[high] == target) {
            return high;
        }
        return -1;
    }
}

 

 另一种情况是旋转数组中存在重复元素的时候，这个时候与上面基本相似，就是加一个判断如果nums[mid]=nums[low]的话，就是让low++，具体代码如下：

 

public class Solution {
    public boolean search(int[] nums, int target) {
        if (nums.length == 0 || nums == null) {
            return false;
        }
        int low = 0;
        int high = nums.length - 1;
        while(low + 1 < high) {
            int mid = low + ((high - low) >> 1);
            if (nums[mid] == target) {
                return true;
            }
            if (nums[mid] > nums[low]) {//前半部分是升序
                if (target >= nums[low] && target <= nums[mid]) {//待查找的元素再升序子序列中
                    high = mid;
                } else {
                    low = mid + 1;
                }
            } else if (nums[mid] < nums[low]){//前半部分不是升序
                if (target >= nums[mid] && target <= nums[high]) {
                    low = mid;
                } else {
                    high = mid - 1;
                }
            } else {
                low++;
            }
        }
        if (nums[low] == target) {
            return true;
        }
        if (nums[high] == target) {
            return true;
        }
        return false;
    }
}

 

 还有一类题目是在旋转数组中查找最小值。题目如下：

假设一个旋转排序的数组其起始位置是未知的（比如0 1 2 4 5 6 7 可能变成是4 5 6 7 0 1 2）。

你需要找到其中最小的元素。

你可以假设数组中不存在重复的元素。

 注意事项

You may assume no duplicate exists in the array.

您在真实的面试中是否遇到过这个题？ Yes
样例
给出[4,5,6,7,0,1,2]  返回 0

 

最开始应该判断nums[low]<nums[high],是的话这个数组就不是旋转数组，那么最小值肯定是第一个元素；如果不是的话首先是没有重复元素的旋转数组当中，这个时候首先要判断nums[mid]>nums[low],如果是的话，最小值肯定在在mid和high之间，令low=mid+1；否则的话领high=mid，代码如下：

 

public class Solution {
    public int findMin(int[] nums) {
        if (nums.length == 0 || nums == null) {
            return -1;
        }
        int low = 0;
        int high = nums.length - 1;
        if (nums[low] < nums[high]) {
            return nums[low];
        }
        int mid;
        while (low < high) {
            mid = low + ((high - low) >> 1);
            if (nums[mid] > nums[high]) {
                low = mid + 1;
            } else {
                high = mid;
            }
        }
        return nums[low];
    }
}

 

 

 

 

如果是存在重复元素的话，题目如下：

假设一个旋转排序的数组其起始位置是未知的（比如0 1 2 4 5 6 7 可能变成是4 5 6 7 0 1 2）。

你需要找到其中最小的元素。

数组中可能存在重复的元素。

 注意事项

The array may contain duplicates.

您在真实的面试中是否遇到过这个题？ Yes
样例
给出[4,4,5,6,7,0,1,2]  返回 0

 

那么判断nums[mid]>nums[high],如果是的话，那么最小值肯定在mid和high中间，然后判断nums[mid]<nums[low]，如果是的话最小值肯定在low和mid中间；否则的话都有可能，这个时候只需要令high--，代码如下：

 

public class Solution {
    public int findMin(int[] nums) {
        int low = 0;
        int high = nums.length - 1;
        if (nums[low] < nums[high]) {
            return nums[low];
        }
        int mid;
        while (low < high) {
            mid = low + ((high - low) >> 1);
            if (nums[mid] > nums[high]) {
                low = mid + 1;
            } else if (nums[mid] < nums[high]) {
                high = mid;
            } else {
                high--;
            }
        }
        return nums[low];
    }
}

 

 其实这几道题边界的判断条件还不是很理解，也就是low和high是小于等于还是小于，这个要回头看一下，但是题目解法理解。

3.杨氏矩阵问题

 　　先看一个题目，74. Search a 2D Matrix，题目如下：

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.
For example,

Consider the following matrix:

[
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
Given target = 3, return true.

 

　　这道题目有很多种解法，首先看一种，由于这个二维数组是递增的。所以可以把它当做一个一维数组，从头到尾进行二分查找，假设二维数组中每一行有n列，那么在一维数组中，下标为x的元素对应在二维数组中就是nums[x/n][x%n],具体的代码如下：

/**
     * 由于数组是有序递增的，那么可以把二维数组转换为一位数组进行操作
     * 假设二维数组每一行有n列，那么一位数组中下标为x的数对应的二维数组中
     * 的数的为matrix[x/n][x%n]，利用二分法对一维数组进行查找即可
     * 时间复杂度为O(log(m*n))
     * @param matrix
     * @param target
     * @return
     */
    public boolean searchMatrix(int[][] matrix, int target) {
        boolean flag = false;
        if (matrix.length == 0 || matrix == null || matrix[0] == null || matrix[0].length == 0) {
            return false;
        }
        int m = matrix.length;
        int n = matrix[0].length;
        int left = 0;
        int right = m * n - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            int num = matrix[mid / n][mid % n];
            if (num == target) {
                flag = true;
                break;
            } else if (num > target) {
                right = mid - 1;
            } else if (num < target) {
                left = mid + 1;
            }
        }
        return flag;
    }

　　

　　另一种解法就是从矩阵的左下角或者右上角开始搜索，以从左下角搜索为例，如果target小于这个数，那么行数减一，如果大于这个数，列数加一。算法的时间复杂度为O(m+n)。具体的代码如下：

 

/**
     * 从左下角开始查找，如果target小于这个数，则行数减一，如果大于这个数，则列数加一
     * 时间复杂度为O(m)+O(n),m为行数，n为列数
     * @param matrix
     * @param target
     * @return
     */
    public boolean searchMatrix(int[][] matrix, int target) {
        boolean flag = false;
        if (matrix.length == 0 || matrix == null || matrix[0] == null || matrix[0].length == 0) {
            return false;
        }
        int m = matrix.length;
        int n = matrix[0].length;
        int i = m - 1;
        int j = 0;
        while (i >= 0 && j < n) {
            if (matrix[i][j] < target) {
                j++;
            } else if (matrix[i][j] > target) {
                i--;
            } else {
                flag = true;
                break;
            }
        }
        return flag;
    }

 

　　还可以将target的值于每一行的第一个元素进行比较，找到第一个不大于target的数，并获得这一行，在这一行进行二分查找，这种解法的时间复杂度是O(logm)+O(logn)，算是时间复杂度最好的解法。具体的代码如下：

 

public class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) {
            return false;
        }
        int low = 0;
        int high = matrix.length - 1;
        int mid = 0;
        while (low + 1 < high) {
            mid = low + ((high - low) >> 1);
            if (matrix[mid][0] == target) {
                return true;
            } else if (matrix[mid][0] > target) {
                high = mid;
            } else {
                low = mid;
            }
        }
        int index = matrix[high][0] <= target ? high : low;
        low = 0;
        high = matrix[0].length - 1;
        while (low + 1 < high) {
            mid = low + ((high - low) >> 1);
            if (matrix[index][mid] == target) {
                return true;
            } else if (matrix[index][mid] > target) {
                high = mid;
            } else {
                low = mid;
            }
        }
        if (matrix[index][low] == target || matrix[index][high] == target) {
            return true;
        }
        return false;
    }
}

 

　　还有一种解法就是对每一行进行二分查找，假设有m行n列,那么时间复杂度就是O(mlog(n))，这个比较简单，所以就不详细介绍了。

　　关于杨氏矩阵的另一种题目就是这个矩阵只是每一行是单调递增的，整体不是，这样的话就没法将二维数组转换成一维数组去操作了，但是还是可以从右上角或是左下角去查找，或者是对每一行进行二分查找。

4.函数的极大值问题

　　直接上题，162. Find Peak Element，具体的题目如下：

 

A peak element is an element that is greater than its neighbors.

Given an input array where num[i] ≠ num[i+1], find a peak element and return its index.

The array may contain multiple peaks, in that case return the index to any one of the peaks is fine.

You may imagine that num[-1] = num[n] = -∞.

For example, in array [1, 2, 3, 1], 3 is a peak element and your function should return the index number 2.

 

 

　　这个题的话就跟函数的极值有关了，首先如果使用线性算法，也就是在O(n)的时间内解决的话，直接比较num[i]>num[i-1]&&num[i]>num[i+1]，注意边界，两个边界，只要num[0]>num[1]或者num[n]>num[n-1]，这时候边界的值就是峰值。具体代码如下：

public class Solution {
    public int findPeakElement(int[] nums) {
        int n = nums.length;
        if (n == 1) {
            return 0;
        }
        //不包含两端的元素
        for (int i = 1; i < n - 1; i++) {
            if (nums[i] > nums[i - 1] && nums[i] > nums[i + 1]) {
                return i;
            }
        }
        if (nums[0] > nums[1]) {
            return 0;
        }
        if (nums[n - 1] > nums[n - 2]) {
            return n - 1;
        }
        return 0;
    }
}

　　

　　另外一种是用二分法求解，首先如果是单调递减，即nums[i]>nums[i+1]，那么就往左边寻找峰值或者i自身就是峰值；如果是单调递增，即nums[i]<nums[i+1],那么就去i右边寻找峰值我们很容易在纸上画出来某个点的四种情况（如下图所示）:

 

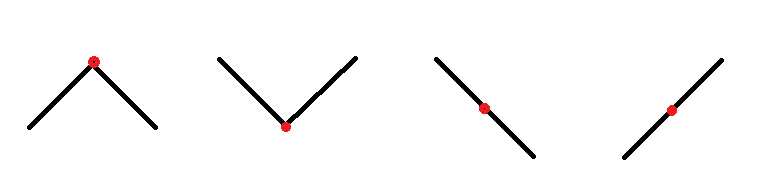
第一种情况：当前点就是峰值，直接返回当前值。

第二种情况：当前点是谷点，不论往那边走都可以找到峰值。

第三种情况：当前点处于下降的中间，往左边走可以到达峰值。

第四种情况：当前点处于上升的中间，往右边走可以达到峰值。

 

 具体代码如下：

public class Solution {
    public int findPeakElement(int[] nums) {
        int n = nums.length;
        if (n == 1) {
            return 0;
        }
        int start = 0;
        int end = nums.length - 1;
        int mid;
        while (start < end) {
            mid = start + ((end - start) >> 1);
            if (nums[mid] > nums[mid + 1]) {
                end = mid;
            } else {
                start = mid + 1;
            }
        }
        return start;
    }
}