数据结构与算法-二叉排序树

Posted 2021-02-22 yfyyy

二叉排序树

1. 基本介绍

二叉排序树：BST，对于二叉排序树的任何一个非叶子结点，要求左子结点的值比当前结点的值小，右子结点的值比当前结点的值大

特别说明：若有相同的值，可以将该结点放在左子结点或右子结点

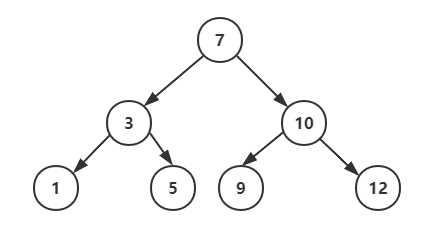
2. 二叉排序树的创建和遍历

public void add(Node node) {
    if(node == null) {
        return;
    }
    if(node.value < this.value) {
        //若左子结点为空
        if(this.left == null) {
            this.left = node;
        }else { //不为空则递归添加
            this.left.add(node);
        }
    }else {
        if(this.right == null) {
            this.right = node;
        }else {
            this.right.add(node);
        }
    }
}

3. 二叉排序树的删除

删除有以下三种情况

• 删除叶子结点（2，5，9，12）
• 删除只有一棵子树的结点（1）
• 删除有两颗子树的结点（7，3，10）

第一种情况，删除叶子结点

• 先找到要删除的结点 targetNode
• 找到要删除结点的父结点 parent
• 确定要删除的结点是其父结点的左孩子还是右孩子 targetNode 与 parent
• 进行删除

第二种情况，删除只有一颗子树的结点

• 先找到要删除的结点 targetNode

• 找到要删除结点的父结点 parent

• 判断要删除结点的子结点是左子结点还是右子结点 targetNode的孩子

• 判断要删除结点是其父结点的左子结点还是右子结点 targetNode 和 parent

• 若要删除的结点有左孩子 targetNode 的孩子

  • 若要删除的结点是其父结点的左孩子 targetNode 是 parent的左孩子时

    parent.left = targetNode.left;

  • 若要删除的结点是其父结点的右孩子 targetNode 是 parent的右孩子时

    parent.right = targetNode.right;

第三种情况，删除有两颗子树的结点

• 先找到要删除的结点 targetNode
• 找到要删除结点的父结点 parent
• 从要删除的结点的右子树找到最小的·结点
• 用一个临时变量将最小结点的值保存
• 删除该最小结点
• targetNode.value = temp

/**
     * 查找要删除的结点
     * @param value 希望删除结点的值
     * @return 如果找到，返回该结点否则返回null
     */
public Node search(int value) {
    if(value == this.value) {   //就是此结点，找到
        return this;
    }else if(value < this.value) {  //若要查找的值小于此结点，向左子树递归查找
        //若左子树为空
        if(this.left == null) {
            return null;
        }
        return this.right.search(value);
    } else {    //若要查找的值不小于当前结点，向右子树递归查找
        if(this.right == null) {
            return null;
        }
        return this.right.search(value);
    }
}

/**
     * 查找要删除结点的父结点
     * @param value 要删除结点的父结点
     * @return 返回要删除结点的父结点，没有则返回null
     */
public Node searchParent(int value) {
    //若当前结点就是要删除结点的父结点，则直接返回
    if((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
        return this;
    }else {
        //若要查找的值小于当前结点的值，并且当前结点的左子结点不为空
        if(value < this.value && this.left != null) {
            return this.left.searchParent(value);       //向左子树递归查找
        }else if(value >= this.value && this.right != null) {
            return this.right.searchParent(value);      //向右子树递归查找
        }else {
            return null;
        }
    }
}

// 删除结点
public void delNode(int value) {
    if (root != null) {
        // 1.需求先去找到要删除的结点 targetNode
        Node targetNode = search(value);
        // 如果没有找到要删除的结点
        if (targetNode == null) {
            return;
        }
        // 如果我们发现当前这颗二叉排序树只有一个结点
        if (root.left == null && root.right == null) {
            root = null;
            return;
        }

        // 去找到targetNode的父结点
        Node parent = searchParent(value);
        // 如果要删除的结点是叶子结点
        if (targetNode.left == null && targetNode.right == null) {
            // 判断targetNode 是父结点的左子结点，还是右子结点
            if (parent.left != null && parent.left.value == value) { // 是左子结点
                parent.left = null;
            } else if (parent.right != null && parent.right.value == value) {// 是由子结点
                parent.right = null;
            }
        } else if (targetNode.left != null && targetNode.right != null) { // 删除有两颗子树的节点
            targetNode.value = delRightTreeMin(targetNode.right);

        } else { // 删除只有一颗子树的结点
            // 如果要删除的结点有左子结点
            if (targetNode.left != null) {
                if (parent != null) {
                    // 如果 targetNode 是 parent 的左子结点
                    if (parent.left.value == value) {
                        parent.left = targetNode.left;
                    } else { // targetNode 是 parent 的右子结点
                        parent.right = targetNode.left;
                    }
                } else {
                    root = targetNode.left;
                }
            } else { // 如果要删除的结点有右子结点
                if (parent != null) {
                    // 如果 targetNode 是 parent 的左子结点
                    if (parent.left.value == value) {
                        parent.left = targetNode.right;
                    } else { // 如果 targetNode 是 parent 的右子结点
                        parent.right = targetNode.right;
                    }
                } else {
                    root = targetNode.right;
                }
            }
        }
    }
}

//查找要删除的结点
public Node search(int value) {
    if(root == null) {
        return null;
    }else {
        return root.search(value);
    }
}

//查找父结点
public Node searchParent(int value) {
    if(root == null) {
        return null;
    }else {
        return root.searchParent(value);
    }
}