Yangk's 静态主席树-模板

Posted 2021-02-22 yangkun-

主席树

然后在这先%%%一个B站宝藏up主，数据结构讲的很清楚，主席树这一节也是听了很多很多遍

https://space.bilibili.com/120174936?spm_id_from=333.788.b_765f7570696e666f.1

有些概念来自up主的ppt,主席树的代码习惯也是跟up主学的欸嘿嘿

什么是主席树

主席树是一种可持久化的数据结构一可持久化线段树(因为其有函数的性质也叫函数式线段树)

至于为什么叫主席树呢，在这先膜一下黄嘉泰大佬 (HJT) % % % 剩下自行体会

这篇介绍的是静态主席树，至于带修改主席树以及树上主席树的坑，我以后再补

怎么实现

先抛出一个问题，在线询问时，可能会用到之前修改后的值，但他已经被你后几次的修改覆盖掉了，怎么办，把他们都存下来吗

空间复杂度爆炸的大

但是，可以发现，两版本之间有很多的相同之处，如果能利用上这些相同的部分，那么就可以节省很大一部分空间，使得空间复杂度下降

其实，主席树的本质是好多个线段树，我们利用了前缀的思想，对于每一个前缀建一棵树，降低时间复杂度，然后再利用相同的部分把空间复杂度降下来（相当于每次操作只是多了一条链而不是一颗完整的树），达到高效实现问题的效果

实际上，模板题只是一道静态主席树，利用前缀的思想还可以将主席树与树状数组套在一起，实现带修改主席树，不过这就是后话了

如何利用之前版本相同的内容

我们可以在构建新版本的线段树的时候，把没有变动的部分连回到上一个版本的那个部分上（把他左边的树维护的东西复制一遍给他，然后再修改需要修改的值）

这样就可以实现0浪费了

我看这个图片就非常的形象

图片来自：https://www.cnblogs.com/LonecharmRiver/articles/9087536.html

 

 

 

 

 

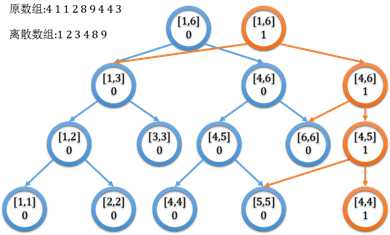
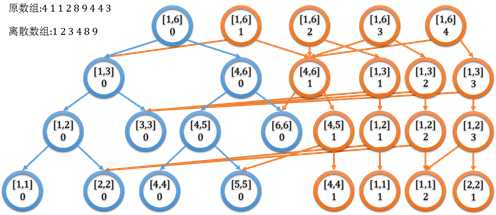
这是模板题 洛谷P3834 POJ-2104 K-th Number的解题思路

在原来的基础上新建一条链 连回另一个子节点 下面我们就来看一下这个题吧

模板题

洛谷P3834 POJ-2104 K-th Number

题目描述

如题，给定 n 个整数构成的序列，将对于指定的闭区间查询其区间内的第 k小值。

输入格式

第一行包含两个正整数 n,m，分别表示序列的长度和查询的个数。

第二行包含 n 个整数，表示这个序列各项的数字。

接下来 m 行每行包含三个整数 l, r, k, 表示查询区间 [l, r]内的第 k小值。

输出格式

输出包含 m行，每行一个整数，依次表示每一次查询的结果

数据范围

1<=n,m<=2e5   -1e9<=a[i]<=1e9

 

朴素做法：每次对[l,r]排序再询问o(mnlogn) 铁定是过不去

HJT大佬做法：对于原序列的每一个前缀[1--i]建立出一棵线段树维护值域上每个数出现的次数，则其树是可减的

插播：权值线段树，对一个值域上的值的个数进行维护的线段树，

对于一段数字序列，每次询问其第K大值

先建树然后对于每次询问递归查找即可。要找的数如果在左子树上，

就递归查找左子树上的第k大;如果在右子树上，那么就递归查找右子树上的.第(k-左子树值)大

只是在这个题里，可持久化与权值线段树联系在一起了，但实际还有很多可持久化的问题是维护的别的东西，所以也不用说是对于实现的方式过于较真，怎么解怎么实现还是要看题目

 

了解了权值线段树，我们就可以切这道题了

首先，我们需要先对数据进行离散化。为什么要离散化呢?因为权值线段树维护的是值域,上值的个数，数据范围是-1e9≤a[i]≤1e9，显然开不出这么大的线段树。因为问题只与数的大小相关，而与数本身是多少无关，所以我们可以对数进行离散化，只保存其大小关系即可

例: 25957 6405 15770 26287 26465离散化结果: 3 1245

然后我们的主要思想是:用主席树构造一颗可持久化权值线段树，对于每个数字，将其离散化后，新建一个版本的权值线段树，然后插入这个离散化后的数字。例如对于上述序列，我们就要依次建立5个版本的权值线段树，分别插入31245这五个数。这就是对原序列的每一个前缀建树’

对于查询操作L，R，我们利用主席树的函数性质，用R那个版本的权值线段树减去L-1那个版本的权值线段树，在得到的权值线段树中查找第K小值就可以了。有点类似前缀和

这样为什么是正确的呢?因为权值线段树储存的是值域,上值的个数，我们用R版本的权值线段树减去L-1版本的权值线段树，得到的就是维护[L,R]上值的个数的权值线段树

得到结论：主席树=权值线段树+可持久化+前缀和

关于如何实现

离散化：vector排序去重，用的时候二分查找

 

排序去重

sort(ve.begin(),ve.end());

ve.erase(unique(ve.begin(),ve.end()),ve.end());

 

getid

int getid(int x){return lower_bound(ve.begin(),ve.end(),x)-ve.begin()+1;}

 

 

如何储存主席树：

主席树和线段树不一样，因为是动态开点，所以找左右儿子不能通过<<1 and<<1|1来实现，但我们可以用一个结构体存下他的儿子节点的编号，因为是动态开点，最后要开多少点我们也不能确定，但一般都开到35-50左右

hjt[i]为树上的节点，cnt为动态开点的计数器，root[i]为根结点编号，一个root[i]就是一个新版本

struct node
{
    int l,r,sum;

}hjt[maxn*40];

int cnt,root[maxn],a[maxn];

 

 

用不用建树？？

这个题不用，因为原来的树是空的

 

两个线段树相减用不用再搞个树

不用，可以在询问的时候边递归边减,

 

再就是以上的问题呢，也不是绝对的，主要是得跟着题走，但基本不变的是 树的储存，insert操作，insert,query调用，离散化（好多都要）

关于代码

插入：

Insert(左，右，上一个版本的根节点编号，当前版本根结点编号，要插入的位置)

先给当前节点分配一段新内存

然后把上一个版本的树的这个位置维护的东西给当前版本复制一遍

把当前节点的编号改为这个新节点

改变当前节点维护的值

递归分别向左右插入

Insert(左，右，上一个版本的左子节点编号，当前版本左子结点编号，要插入的位置)

Insert(左，右，上一个版本的右子节点编号，当前版本右子结点编号，要插入的位置)

void insert(int l,int r,int pre,int &now,int p)
{
    hjt[++cnt]=hjt[pre];
    now=cnt;
    hjt[now].sum++;
    if(l==r) return ;
    int mid=(l+r)>>1;
    if(p<=mid) insert(l,mid,hjt[pre].l,hjt[now].l,p);
    else insert(mid+1,r,hjt[pre].r,hjt[now].r,p);
}

 

 

查询：

Query(左，右，上一个版本的根节点编号，当前版本根结点编号，第几大)

如果到了叶子节点，找到答案

Temp=两版本相减得到的树的左子节点有多少个数

如果大于k，证明第k大在左子树，否则在右子树 （hjt[pre].l,hjt[now].l同步进行，同步递归）

如果在右子树，那么我们应该找的是第k=temp大，因为左子树有k个

int query(int l,int r,int pre,int now,int k)
{
    if(l==r) return l;
    int mid=(l+r)>>1;
    int tem=hjt[hjt[now].l].sum-hjt[hjt[pre].l].sum;
    if(k<=tem) return query(l,mid,hjt[pre].l,hjt[now].l,k);
    else return query(mid+1,r,hjt[pre].r,hjt[now].r,k-tem);
}

 

 

主函数

插入

Insert(1，n,上一个数字的那个版本，当前数字版本，找离散后的位置也就是要插入的地方)

    for(int i=1;i<=n;i++)
    {
        insert(1,n,root[i-1],root[i],getid(a[i]));
    }

 

查询

Query(1，n，前一个版本，当前版本，第k大)-1（ve下标从0开始）

       

 printf("%d
",ve[query(1,n,root[l-1],root[r],k)-1]);

 

 

完整代码：

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 #define ll long long
 4 const int mod = 1e9 + 7;
 5 const int inf = 0x3f3f3f3f;
 6 const int maxn = 200009;
 7 vector<int> ve;
 8 struct node
 9 {
10     int l, r, sum;
11 } hjt[maxn * 40];
12 int cnt, root[maxn], a[maxn];
13 
14 int getid(int x) { return lower_bound(ve.begin(), ve.end(), x) - ve.begin() + 1; }
15 
16 void insert(int l, int r, int pre, int &now, int p)
17 {
18     hjt[++cnt] = hjt[pre];
19     now = cnt;
20     hjt[now].sum++;
21     if (l == r)  return;
22     int mid = (l + r) >> 1;
23     if (p <= mid)  insert(l, mid, hjt[pre].l, hjt[now].l, p);
24     else  insert(mid + 1, r, hjt[pre].r, hjt[now].r, p);
25 }
26 
27 int query(int l, int r, int pre, int now, int k)
28 {
29     if (l == r)
30         return l;
31     int mid = (l + r) >> 1;
32     int tem = hjt[hjt[now].l].sum - hjt[hjt[pre].l].sum;
33     if (k <= tem)  return query(l, mid, hjt[pre].l, hjt[now].l, k);
34     else  return query(mid + 1, r, hjt[pre].r, hjt[now].r, k - tem);
35 }
36 
37 int main()
38 {
39     //  freopen("in.in","r",stdin);
40     int n, m;
41     scanf("%d%d", &n, &m);
42     for (int i = 1; i <= n; i++)
43     {
44         scanf("%d", &a[i]);
45         ve.push_back(a[i]);
46     }
47     sort(ve.begin(), ve.end());
48     ve.erase(unique(ve.begin(), ve.end()), ve.end());
49     for (int i = 1; i <= n; i++)
50     {
51         insert(1, n, root[i - 1], root[i], getid(a[i]));
52     }
53     int l, r, k;
54     while (m--)
55     {
56         scanf("%d%d%d", &l, &r, &k);
57         printf("%d
", ve[query(1, n, root[l - 1], root[r], k) - 1]);
58     }
59     return 0;
60 }

 

学之前呢，听着这个算法非常的高大上，非常的难啊，但是真正过掉题并且能把解决问题的思路，过程口胡出来，（最好是边念叨边写）确实是很有成就感的，而且会越来越熟练，就不存在每次写线段树都在模板上改，然后时间久了就看不懂代码了的情况（至少现在是没有）

总结，也不是说理解了思维，过掉了模板题就是说会了这个算法了，只能说是了解了基本的过程，并且希望下次碰到心里能不慌，能撸出来是最好的，做不出来也只能说是不够熟练，谁能一口气吃个胖子呢，还是得慢慢理解代码，把他磨成自己的

好像每一次卡题之后的ac都很是欣慰，感觉对他的理解又多了那么一点点hhhhhh