最长公共子序列

Posted 2021-02-21 jason66661010

最长公共子序列

longest common subsequence，LCS

说明：子序列中的字符与子字符串中的字符不同，它们不需要是连续的，例如：

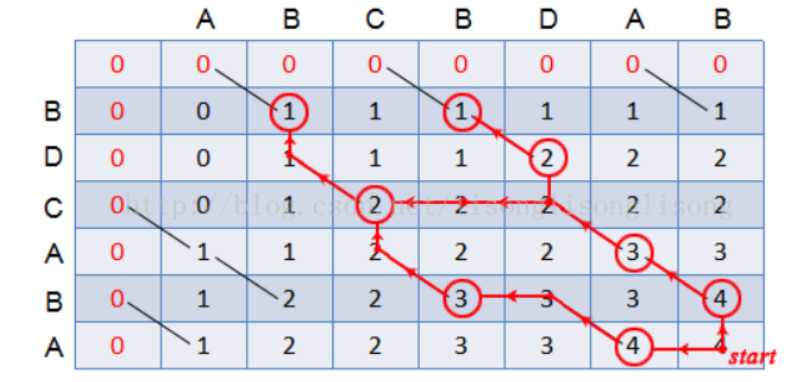
字符串1：BDCABA；字符串2：ABCBDAB

最长公共子序列长度为4，最长公共子序列是：BCBA

算法求解——动态规划

最优子结构

设两个字符串分别是X,Y；其中X长度为n，Y的长度为m。

LCS(Xn,Ym)就是求出X、Y的最长公共子序列，而其中就有三个子问题：

考虑X与Y的最后一个字符是否一样，我们可以将情况分为三类：

1.X与Y的最后一个字符一样，则LCS(Xn,Ym)=LCS（Xn-1,Ym-1）+1

2.X与Y的最后一个字符不一样，LCS(Xn,Ym)=LCS（Xn-1,Ym）

2.X与Y的最后一个字符不一样，LCS(Xn,Ym)=LCS（Xn,Ym-1）

重叠子问题

 

例如当LCS(Xn-1,Ym)最后的字符不相同时，问题就包含LCS（Xn-1,Ym-1），LCS（Xn-2,Ym），所以要使用动态规划进行记忆化搜索

 

代码解决

LCS可能存在不唯一的多条路径：

1. 如果格子dp[i][j]对应的X[i-1] == Y[j-1]，则把这个字符放入 LCS 中，并跳入dp[i-1][j-1]中继续进行判断；

2. 如果格子dp[i][j]对应的 X[i-1] ≠ Y[j-1]，则比较dp[i-1][j]和dp[i][j-1]的值，跳入值较大的格子继续进行判断；

3. 直到 i 或 j 小于等于零为止，倒序输出 LCS 。

如果出现dp[i-1][j]等于dp[i][j-1]的情况，说明最长公共子序列有多个，故两边都要进行回溯（这里用到递归）。

 

 

 

 

 代码：

#include<iostream>
#include<string>
#include<cstring>
#include<algorithm>
#include<set>
using namespace std;
int dp[1000][1000];
set<string>list;
void traceBack(int i, int j, string a,string b,string str)
{
    while (dp[i][j])
    {
         if (a[i-1]==b[j-1])//从dp[i-1][j-1]开始可能存在LCS中的字符,int i = a.size(), j = b.size();此时a[i],b[j]无字符，所以在dp[i][j]判断dp[i-1][j-1]，在dp[i-1][j-1]判断dp[i-2][j-2]
            i--, j--, str += a[i];
         else
         {
             if (dp[i - 1][j] > dp[i][j - 1])
                 i--;
             else if (dp[i - 1][j] < dp[i][j - 1])
                 j--;
             else//dp[i - 1][j] == dp[i][j - 1]最长公共子序列有多个，故两边都要进行回溯
             {
                 traceBack(i - 1, j, a,b, str);
                 traceBack(i, j-1, a, b,str);
                 return;
             }
        }
    }
    reverse(str.begin(), str.end());
    list.insert(str);
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    string a, b, t = "";
    cin >> a >> b;
    for (int i = 1; i <= a.size(); i++)
        for (int j = 1; j <= b.size(); j++)
            if (a[i - 1] == b[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;//X与Y的最后一个字符一样，则LCS(Xn,Ym)=LCS（Xn-1,Ym-1）+1
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);//X与Y的最后一个字符不一样,取二者最大值
    int i = a.size(), j = b.size();
    traceBack(i, j, a,b, t);
    cout << dp[a.size()][b.size()] <<endl;
    for (auto it = list.begin(); it != list.end(); it++)
        cout << *it << endl;

}

参考：

https://blog.csdn.net/weixin_30819085/article/details/95597662
https://blog.csdn.net/dbbaq24022/article/details/101331486?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2