二分查找模版

Posted 2021-02-21 zhihaospace

二分查找模版

• 来源：公众号 labuladong

• 注意： int mid = left + (right - left) / 2; 这么写而不是 int mid = (left + right) >> 1; 是由于left加right可能整数溢出

public class BinarySearch {
    
    ////找到nums数组中的一个和target值相同的位置，未找到则返回-1（适用于非重复值数组）
    int binary_search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while(left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if(nums[mid] == target) {
                // 直接返回
                return mid;
            }
        }
        // 直接返回
        return -1;
    }

    //找到nums数组中最左边一个和target值相同的位置，未找到则返回-1，（适用于重复值数组）
    int left_bound(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] == target) {
                // 别返回，收缩左侧边界
                right = mid - 1;
            }
        }
        // 最后要检查 left 越界的情况
        if (left >= nums.length || nums[left] != target)
            return -1;
        return left;
    }


    //找到nums数组中最右边一个和target值相同的位置，未找到则返回-1，（适用于重复值数组）
    int right_bound(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] == target) {
                // 别返回，收缩右侧边界
                left = mid + 1;
            }
        }
        // 最后要检查 right 越界的情况
        if (right < 0 || nums[right] != target)
            return -1;
        return right;
    }
    
}

• 例题：https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/

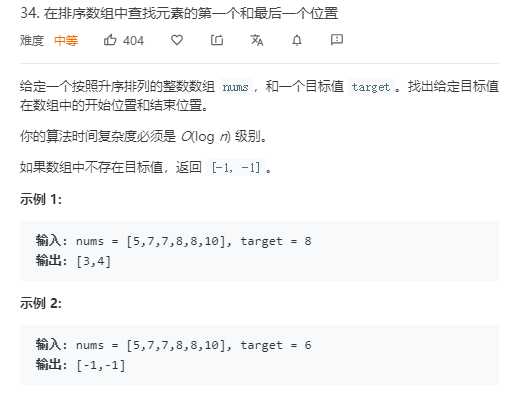
public class P34FindFirstAndLastPositionOfElementInSortedArray {
    /**
     * 输入: nums = [5,7,7,8,8,10], target = 8
     * 输出: [3,4]
     */
    public static void main(String[] args) {
        Solution solution = new P34FindFirstAndLastPositionOfElementInSortedArray().new Solution();
        // TO TEST
        int[] ints = solution.searchRange(new int[]{5, 7, 7, 8, 8, 10}, 8);
        for (int anInt : ints) {
            System.out.print(anInt + ",");
        }
    }

    //leetcode submit region begin(Prohibit modification and deletion)
    class Solution {
        public int[] searchRange(int[] nums, int target) {

            int[] arr = new int[]{-1, -1};
            int len = nums.length;
            if (len == 0) {
                return arr;
            }

            arr[0] = left_bound(nums, target);
            arr[1] = right_bound(nums, target);
            return arr;
        }

        //找到nums数组中最左边一个和target值相同的位置，未找到则返回-1，（适用于重复值数组）
        int left_bound(int[] nums, int target) {
            int left = 0, right = nums.length - 1;
            while (left <= right) {
                int mid = left + (right - left) / 2;
                if (nums[mid] < target) {
                    left = mid + 1;
                } else if (nums[mid] > target) {
                    right = mid - 1;
                } else if (nums[mid] == target) {
                    // 别返回，收缩左侧边界
                    right = mid - 1;
                }
            }
            // 最后要检查 left 越界的情况
            if (left >= nums.length || nums[left] != target)
                return -1;
            return left;
        }


        //找到nums数组中最右边一个和target值相同的位置，未找到则返回-1，（适用于重复值数组）
        int right_bound(int[] nums, int target) {
            int left = 0, right = nums.length - 1;
            while (left <= right) {
                int mid = left + (right - left) / 2;
                if (nums[mid] < target) {
                    left = mid + 1;
                } else if (nums[mid] > target) {
                    right = mid - 1;
                } else if (nums[mid] == target) {
                    // 别返回，收缩右侧边界
                    left = mid + 1;
                }
            }
            // 最后要检查 right 越界的情况
            if (right < 0 || nums[right] != target)
                return -1;
            return right;
        }
    }
}