树状数组

Posted 2021-02-20 et3-tsy

树状数组

资料借鉴:

https://www.luogu.com.cn/problemnew/solution/P3374

适用范围

单次查询时间复杂度：O(logN)

区间和、区间异或和、区间乘积和静态RMQ

支持单点、区间修改

形式

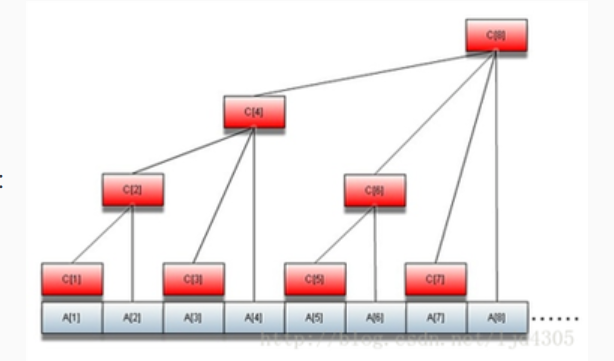
红点是树状数组，白点是原信息数组

对于树状数组中的每一个红点i，应有：

算上其本身的讯息，总共存储了2^k的白点信息，并且白点信息是连续的

其中k表示，k取最大时，能使得x能被2^k整除

观察上面红点，它有一个神奇的特点：

对于每个i而言，一旦i被修改，i+2^k必会跟着一起进行相应变换

使用

1.k的计算（函数lowbit）

x&-x计算2^{k,其中k表示，k取最大时，能使得x能被2}k整除（这里要用到补码的知识进行证明，略）

2.维护和初始化

对于白点的原信息，我们可以看作是对位置i，进行了增加white[i]的维护

所以我们该如何维护嘞？我们先看对一个点的维护

利用上面红点带来的性质，我们不难发现，当i被修改，i+2^{k也被修改；同理i+2}k被修改，那么...

所以，我们很好地可以得到维护代码

void renew(int x,int k)//x指当前修改的位置，k是维护值
{
	for(;x<=n;x+=(x&-x))tree[x]+=k;//这里维护为区段求和
}

3.查询

对于树状数组的每一个点而言，它总共存储了2^k的原始点信息，并且他们是连续的

为了查询点i的前缀和，而i又只能保存2^k的信息，

所以我们将i减去2^{k，进一步去找点（i-2}k）的前缀和，并不断重复上述过程

查询代码:

int query(int x)//查询位置为x的前缀和
{
	int t=0;//累加器
	for(;x;x-=(x&-x))t+=tree[x];
	return t;
}

RMQ

用树状数组写RMQ实在没有优势

存储空间上与线段树相当，建立的复杂度也相当，但是查询开销要到O(logn*logn)，慢太多

如果是追求效率查询又不如ST表

有点鸡肋，贴一个大佬博客详细介绍树状数组求RMQ的方法

大佬博客：https://blog.csdn.net/ljsspace/article/details/6674273

原数组&&差分数组

对于树状数组而言，查询和修改只能至多有一个是对区间进行的

对于洛谷的两个模版而言，很好地诠释了这一点

1，对单点修改，对区段查询，要将树状数组建立在原数组上

2，对区段修改，对单点查询，树状数组建立在差分数组上

如果操作都是对区间进行的，那么只能把线段树掏出来了

---

洛谷树状数组模版1 P3374 对单点修改 对区段查询

树状数组建立在原数组上

#include<iostream>
#include<cstring>
#include<cstdio>
#define INF 0x3f3f3f3f
#define maxn 500005
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
inline int read()
{
    int ans=0;
    char last=‘ ‘,ch=getchar();
    while(ch<‘0‘|ch>‘9‘)last=ch,ch=getchar();
    while(ch>=‘0‘ && ch<=‘9‘)ans=ans*10+ch-‘0‘,ch=getchar();
    if(last==‘-‘)ans=-ans;
	return ans;
}
int tree[maxn];
int n,m;
void renew(int x,int k)
{
    for(;x<=n;x+=(x&-x))tree[x]+=k;
}
int cal(int x)
{
    int t=0;
    for(;x;x-=(x&-x))t+=tree[x];
    return t;
}
int main()
{
	n=read(),m=read();
	memset(tree,0,sizeof(tree));
	for(int i=1;i<=n;i++)
	{
	    int cur=read();
	    renew(i,cur);
	}
	for(int i=1;i<=m;i++)
	{
	    int a=read(),b=read(),c=read();
	    if(a==1)renew(b,c);
	    else std::cout<<cal(c)-cal(b-1)<<‘
‘;
	}
	return 0;
}

洛谷树状数组模版2 P3368 对区段修改 对单点查询

树状数组建立在差分数组上

#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#define INF 0x3f3f3f3f
#define maxn 500005
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
inline int read()
{
    int ans=0;
    char last=‘ ‘,ch=getchar();
    while(ch<‘0‘|ch>‘9‘)last=ch,ch=getchar();
    while(ch>=‘0‘ && ch<=‘9‘)ans=ans*10+ch-‘0‘,ch=getchar();
    if(last==‘-‘)ans=-ans;
    return ans;
}
int tree[maxn];
int save[maxn];
int n,m;
void renew(int x,int k)
{
    for(;x<=n;x+=(x&-x))tree[x]+=k;
}
void seg(int l,int r,int k)
{
    renew(l,k);
    renew(r+1,-k);
}
int cal(int x)
{
    int t=0;
    for(;x;x-=(x&-x))t+=tree[x];
    return t;
}
int main()
{
	n=read(),m=read();
	memset(tree,0,sizeof(tree));
	memset(save,0,sizeof(save));
	int pre=0,temp=0;
	for(int i=1;i<=n;i++)//读入，并且计算差分
	{
	    int cur=read();
	    pre=cur;
	    cur-=temp;
	    renew(i,cur);
	    temp=pre;
	}
	for(int i=1;i<=m;i++)
	{
	    int a,b,c;
	    a=read();
	    if(a==1)
	    {
	        a=read(),b=read(),c=read();
	        seg(a,b,c);
	    }
	    else
	    {
	        a=read();
	        std::cout<<cal(a)<<‘
‘;
	    }
	}
	return 0;
}

康托排序模版 P5367

最开始我还以为二分能过，用了vector和lower_bound，忽然想起vector删除复杂度为n...

其实也可以掏线段树，只不过我懒得写pushdown，lazy—tag这些

so，下面是使用

#include<iostream>
#include<cstring>
#include<cstdio>
#define maxn 1000005
#define ll long long int
#define mod 998244353
using namespace std;
inline int read()
{
    int ans=0;
    char last=‘ ‘,ch=getchar();
    while(ch<‘0‘|ch>‘9‘)last=ch,ch=getchar();
    while(ch>=‘0‘ && ch<=‘9‘)ans=ans*10+ch-‘0‘,ch=getchar();
    if(last==‘-‘)ans=-ans;
    return ans;
}
ll n;
ll a[maxn],A[maxn];
ll ans(1);
void add(ll x,ll k)
{
    for(;x<=n;x+=(x&-x))a[x]+=k;
}
ll query(ll x)
{
    ll t=0;
    for(;x;x-=(x&-x))t+=a[x];
    return t;
}
int main()
{
    n=read();
    A[0]=1;
    memset(a,0,sizeof(a));
    for(int i=1;i<=n;i++)
    {
        A[i]=A[i-1]*i%mod;
        add(i,1);
    }
    for(int i=1;i<=n;i++)
    {
        ll x=read();
        ans=(ans+(query(x)-1)*A[n-i])%mod;
        add(x,-1);
    }
    std::cout<<ans;
    return 0;
}